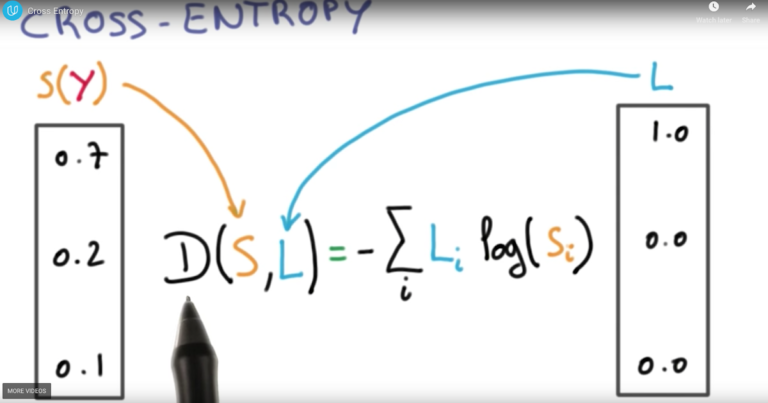
Я нашел это на курсе глубокого обучения Udacity от Google. Я собираюсь подробнее остановиться на этих заметках, чтобы помочь вам лучше понять концепцию.

Обозначение:
D(S,L) — перекрестная энтропия
L – метка, предназначенная для обучения
S (Y) — это выход softmax с точки зрения вероятности для каждого класса для полиномиальной логистической классификации.

Почему она называется полиномиальной логистической классификацией?

Давайте посмотрим на рисунок ниже. Есть входной вектор X, с помощью которого мы обучаем линейный модель также называется логистика модель регрессии – Wx + b. Это создает логит, также известный как баллы Y, которые затем передаются в активацию softmax для получения вероятностного вывода.

Линейная бинарная классификация называется биномиальной логистической классификацией.

Мультиномиальная используется в связи с тем, что существует более 2 классов (по сравнению с биномиальной или бинарной классификацией).

————-

Давайте поможем вам понять математику кросс-энтропии. В основном это функция вывода, генерируемого сетью, и фактических меток. Помните, что он асимметричен из-за используемого неприятного термина журнала. Причина, по которой мы берем журнал вывода softmax, а не метки, заключается в том, что метки являются одноразовыми (содержат серию 0 и одну 1). Логарифм 0 асимптотически стремится к -бесконечности, как показано ниже –

Вот как выглядит функция потерь, когда вы делаете это для каждого действительного входа и метки в сети.

Теперь нам нужно настроить большую матрицу W (веса сети), используя эту функцию потерь, усредненную по всей сети. Один из способов сделать это — использовать градиентный спуск.

Предположим, что ваша сеть имеет 2 веса (2-мерное пространство), нам нужно найти оптимальное численное решение задачи, где значение функции потерь минимально (внутренний красный кружок) для набора значений веса 1 и веса 2. Как мы делаем это?

В основном мы используем технику градиентного спуска. Мы берем производную потери в разных точках, производная дает вам направление изменения, если производная равна -ve, ваш наклон уменьшается (вы прогрессируете в нисходящем направлении), что это будет делать, так это удерживать вас на курсе, пока вы не достигнете минимума функции потерь, как показано на рисунке. Однако, если вы находитесь на подъеме за точкой центра тяжести функции потерь, показанной на рисунке, вы будете двигаться в отрицательном направлении по оси X, пока не достигнете точки минимума.

Я дополню это другой статьей с небольшим количеством математики, следите за обновлениями 🙂