Знаете, что было бы круто? Если бы нам не нужны были все эти помеченные данные для обучения наших моделей. Я имею в виду, что маркировка и категоризация данных требует слишком много работы. К сожалению, без них невозможно обучить большинство существующих моделей, от машин опорных векторов до сверточных нейронных сетей.
За исключением небольшой группы алгоритмов, которые они могут. Заинтригован? Это называется неконтролируемое обучение. Неконтролируемое обучение самостоятельно выводит функцию из неразмеченных данных. Наиболее известными неконтролируемыми алгоритмами являются алгоритмы K-Means, которые широко используются для кластеризации данных в группы и PCA, что является решением для уменьшения размерности. K-Means и PCA, вероятно, являются двумя лучшими когда-либо придуманными алгоритмами машинного обучения. И что делает их еще лучше, так это их простота. Я имею в виду, что если вы их поймете, вы все будете такие: «Почему я не подумал об этом раньше?»
Следующий вопрос, который приходит нам в голову: «Существует ли неконтролируемая нейронная сеть?». Вы, наверное, знаете ответ из названия поста.
Автоэнкодеры.
Для лучшего понимания автоэнкодеров я приведу некоторый код вместе с объяснением. Обратите внимание, что мы будем использовать Pytorch для создания и обучения нашей модели.
import torch
from torch import nn, optim
from torch.autograd import Variable
from torch.nn import functional as F
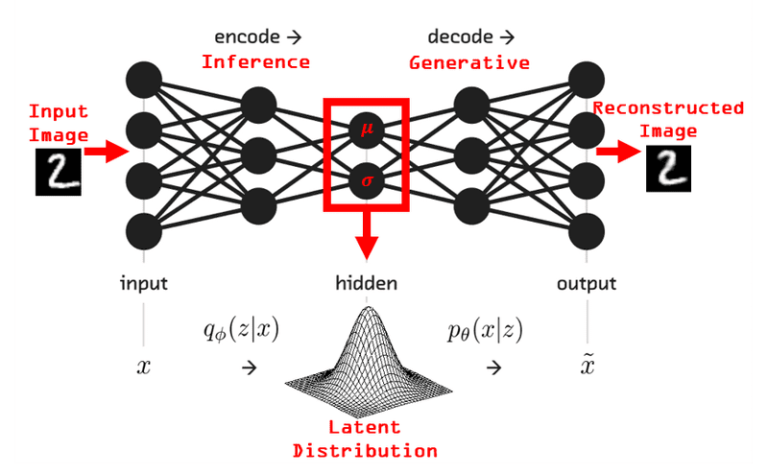
Автоэнкодеры — это простые нейронные сети, вывод которых является их вводом. Просто как тот. Их цель — научиться восстанавливать входные данные. Но насколько это полезно? Хитрость заключается в их структуре. Первая часть сети — это то, что мы называем кодировщиком. Он получает ввод и кодирует его в скрытом пространстве более низкого измерения. Вторая часть (декодер) берет этот вектор и декодирует его, чтобы получить исходный ввод.

Нейронные сети автоэнкодера для коррекции выбросов в биометрической идентификации на основе ЭКГ
Скрытый вектор в середине — это то, что нам нужно, так как это сжатый
представление ввода. И приложений много, например:
-
Сжатие
-
Уменьшение размерности
Более того, ясно, что мы можем применять их для воспроизведения тех же, но немного других или даже лучших данных. Примеры:
-
Шумоподавление данных: предоставьте им зашумленное изображение и научите их выводить такое же изображение, но без шума.
-
Увеличение обучающих данных
-
Обнаружение аномалий: обучайте их на одном классе, чтобы каждая аномалия давала большую ошибку реконструкции.
Однако автоэнкодеры сталкиваются с теми же проблемами, что и большинство нейронных сетей. Они склонны к переоснащению и страдают от проблемы исчезающего градиента. Есть ли решение?
Вариационный автоэнкодер (VAE)
Вариационный автоэнкодер — довольно хорошая и элегантная попытка. По сути, это добавляет случайности, но не совсем точно.
Давайте объясним это дальше. Вариационные автоэнкодеры обучены изучать распределение вероятностей, которое моделирует входные данные, а не функцию, которая отображает входные и выходные данные. Это тогда образцы точки из этого распределения и передать их в декодер для создания новых выборок входных данных. Но подождите минутку. Когда я слышу о распределении вероятностей, на ум приходит только одно: Байес. И да, байесовское правило является основным принципом еще раз. Кстати, я не хочу преувеличивать, но формула Байеса — лучшее из когда-либо созданных уравнений. И я не шучу. Это повсюду. Если вы не знаете, что это такое, пожалуйста, посмотрите. Отбросьте эту статью и узнайте, что такое Байес. Я прощу тебя.
Вернемся к вариационным автоэнкодерам. Я думаю, что следующее изображение проясняет ситуацию:

Синтез текстуры с рекуррентным вариационным автокодировщиком
Вот оно. Стохастическая нейронная сеть. Прежде чем мы создадим собственный пример, генерирующий новые изображения, уместно обсудить еще несколько деталей.
Одним из ключевых аспектов VAE является функция потерь. Чаще всего он состоит из двух компонентов. Потери при реконструкции измеряют, насколько восстановленные данные отличаются от исходных данных (например, бинарная перекрестная энтропия). KL-дивергенция пытается упорядочить процесс и сделать реконструированные данные как можно более разнообразными.
def loss_function(recon_x, x, mu, logvar) -> Variable:
BCE = F.binary_cross_entropy(recon_x, x.view(-1, 784))
KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
KLD /= BATCH_SIZE * 784
return BCE + KLD
Другим важным аспектом является то, как обучать модель. Трудность возникает из-за того, что переменные, как известно, детерминированы, но случайный и градиентный спуск обычно так не работают. Чтобы решить эту проблему, мы используем репараметризацию. Скрытый вектор (z) будет равен обученному среднему (μ) нашего распределения плюс обученному стандартному отклонению (σ), умноженному на эпсилон (ε), где ε соответствует нормальному распределению. Мы перепараметризируем выборки так, чтобы случайность не зависела от параметров.
def reparameterize(self, mu: Variable, logvar: Variable) -> Variable:
if self.training:
std = logvar.mul(0.5).exp_()
eps = Variable(std.data.new(std.size()).normal_())
return eps.mul(std).add_(mu)
else:
return mu
Генерация изображений с помощью AutoEncoders
В нашем примере мы попытаемся сгенерировать новые изображения с помощью вариационного автоматического кодировщика. Мы собираемся использовать набор данных MNIST, а реконструированные изображения будут рукописными числовыми цифрами. Как я уже говорил, я использую Pytorch в качестве фреймворка без особых причин, кроме ознакомления. Во-первых, мы должны определить наши слои.
def __init__(self):
super(VAE, self).__init__()
self.fc1 = nn.Linear(784, 400)
self.relu = nn.ReLU()
self.fc21 = nn.Linear(400, 20)
self.fc22 = nn.Linear(400, 20)
self.fc3 = nn.Linear(20, 400)
self.fc4 = nn.Linear(400, 784)
self.sigmoid = nn.Sigmoid()
Как видите, мы будем использовать очень простую сеть только с плотными (линейными в случае pytorch) слоями. Следующим шагом является создание функции, которая запускает кодировщик и декодер.
def encode(self, x: Variable) -> (Variable, Variable):
h1 = self.relu(self.fc1(x))
return self.fc21(h1), self.fc22(h1)
def decode(self, z: Variable) -> Variable:
h3 = self.relu(self.fc3(z))
return self.sigmoid(self.fc4(h3))
def forward(self, x: Variable) -> (Variable, Variable, Variable):
mu, logvar = self.encode(x.view(-1, 784))
z = self.reparameterize(mu, logvar)
return self.decode(z), mu, logvar
Это всего лишь несколько строк кода Python. Ничего страшного. Наконец, мы можем обучить нашу модель и увидеть сгенерированные изображения.
Краткое напоминание: Pytorch имеет динамический график, в отличие от tensorflow, что означает, что код выполняется на лету. Нет необходимости создавать график, а затем компилировать и выполнять его, Tensorflow недавно представил вышеуказанную функциональность со своим нетерпеливый режим исполнения.
optimizer = optim.Adam(model.parameters(), lr=1e-3)
def train(epoch):
model.train()
train_loss = 0
for batch_idx, (data, _) in enumerate(train_loader):
data = Variable(data)
optimizer.zero_grad()
recon_batch, mu, logvar = model(data)
loss = loss_function(recon_batch, data, mu, logvar)
loss.backward()
train_loss += loss.data(0)
optimizer.step()
def test(epoch):
model.eval()
test_loss = 0
for i, (data, _) in enumerate(test_loader):
data = Variable(data, volatile=True)
recon_batch, mu, logvar = model(data)
test_loss += loss_function(recon_batch, data, mu, logvar).data(0)
for epoch in range(1, EPOCHS + 1):
train(epoch)
test(epoch)
Когда обучение завершено, мы выполняем тестовую функцию, чтобы проверить, насколько хорошо работает модель. На самом деле, получилось довольно неплохо, и сконструированные изображения почти идентичны оригиналу, и я уверен, что никто не смог бы отличить их друг от друга, не зная всей истории.
На изображении ниже показаны исходные фотографии в первом ряду и обработанные во втором.

Неплохо, не правда ли?
Для получения более подробной информации об AutoEncoders, вы должны проверить модуль 5 Глубокое обучение с Tensorflow курс от edX.
Прежде чем мы закроем этот пост, я хотел бы представить еще одну тему. Как мы видели, вариационный автоэнкодер смог генерировать новые изображения. Это классическое поведение генеративной модели. Генеративные модели генерируют новые данные. С другой стороны, дискриминационные модели классифицируют или различают существующие данные по классам или категориям.
Перефразируя это с помощью некоторых математических терминов: генеративная модель изучает совместное распределение вероятностей p(x,y), а дискриминативная модель изучает условное распределение вероятностей p(y|x).
На мой взгляд, генеративные модели гораздо интереснее, поскольку они открывают двери для стольких возможностей, от расширения данных до моделирования возможных будущих состояний. Но об этом в следующем посте. Возможно, в посте об относительно новом типе генеративной модели, называемой генеративно-состязательной сетью.
А пока продолжайте изучать ИИ.
* Раскрытие информации: Обратите внимание, что некоторые из приведенных выше ссылок могут быть партнерскими ссылками, и без дополнительной оплаты для вас мы будем получать комиссию, если вы решите совершить покупку после перехода по ссылке.