Этот пост в блоге является второй частью серии статей о моделях смесей процесса Дирихле. В предыдущей статье мы рассмотрели несколько методов кластерного анализа и обсудили некоторые проблемы/ограничения, возникающие при их использовании. Кроме того, мы кратко представили модели смеси процессов Дирихле, рассказали, почему они полезны, и представили некоторые из их применений.

Обновление: платформа машинного обучения Datumbox теперь имеет открытый исходный код и бесплатна для скачать. Ознакомьтесь с пакетом com.datumbox.framework.machinelearning.clustering, чтобы увидеть реализацию смешанных моделей процессов Дирихле в Java.

Поначалу модели смеси процесса Дирихле могут быть немного трудными для понимания, прежде всего потому, что они представляют собой бесконечные модели смесей с множеством различных представлений. К счастью, хороший способ подойти к этому вопросу — начать с моделей конечных смесей с распределением Дирихле, а затем перейти к бесконечным моделям.

Следовательно, в этой статье я кратко представлю некоторые важные распределения, которые нам понадобятся, мы будем использовать их для построения модели Дирихле Априор с полиномиальным правдоподобием, а затем мы перейдем к модели конечных смесей, основанной на распределении Дирихле.

1. Бета-версия

Бета-распределение представляет собой семейство непрерывных распределений, которое определено в интервале (0,1). Он параметризуется двумя положительными параметрами a и b, и его форма сильно зависит от выбора этих двух параметров.

Рисунок 1: Бета-распределение для различных параметров a, b

Бета-распределение обычно используется для моделирования распределения вероятностей и имеет следующую плотность вероятности:

Уравнение 1: Бета PDF

Где Γ(x) — гамма-функция, а a, b — параметры распределения. Бета обычно используется как распределение значений вероятности и дает нам вероятность того, что смоделированная вероятность равна определенному значению P = p0. По своему определению бета-распределение способно моделировать вероятность бинарных результатов, которые принимают значения true или false. Параметры a и b можно рассматривать как псевдосчетчики успехов и неудач соответственно. Таким образом, бета-распределение моделирует вероятность успеха при условии a успехов и b неудач.

2. Распределение Дирихле

Распределение Дирихле является обобщением бета-распределения для нескольких исходов (или, другими словами, используется для событий с множественными исходами). Он параметризован k параметрами a_я который должен быть положительным. Распределение Дирихле равно бета-распределению, когда количество переменных k = 2.

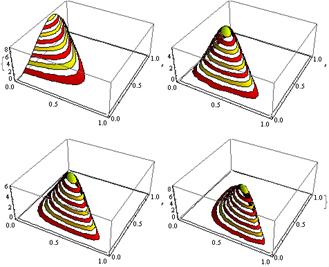
Рисунок 2: Распределение Дирихле для различных a_я параметры

Распределение Дирихле обычно используется для моделирования распределения вероятностей и имеет следующую плотность вероятности:

Уравнение 2: PDF Дирихле

Где Γ(x) — гамма-функция, p_я принимают значения в (0,1) и Σp_я=1. Распределение Дирихле моделирует совместное распределение p_я и дает вероятность P₁=р₁,П₂=р₂,….,П_к-1=р_к-1 с П_к=1 – ΣP_я. Как и в случае с бета-версией,_я параметры можно рассматривать как псевдосчетчики появлений каждого i-го события. Распределение Дирихле используется для моделирования вероятности возникновения k конкурирующих событий и часто обозначается как Дирихле (а).

3. Приор Дирихле с мультиномиальным правдоподобием

Как упоминалось ранее, распределение Дирихле можно рассматривать как распределение по распределениям вероятностей. В случаях, когда мы хотим смоделировать вероятность возникновения k событий, можно использовать байесовский подход. Полиномиальное правдоподобие и априоры Дирихле .

Ниже мы можем увидеть графическую модель такой модели.

Рисунок 3: Графическая модель априоров Дирихле с мультиномиальным правдоподобием

В приведенной выше графической модели α – это размерный вектор ak с гиперпараметрами априоров Дирихле, p – вектор размерности ak со значениями вероятности и x_я является скалярным значением от 1 до k, которое говорит нам, какое событие произошло. Наконец, мы должны отметить, что P следует распределению Дирихле, параметризованному вектором α, и, таким образом, P ~ Дирихле (α), в то время как x_я переменные следуют дискретному распределению (полиномиальному), параметризованному вектором p вероятностей. Подобные иерархические модели можно использовать в классификации документов для представления распределения частоты ключевых слов по разным темам.

4. Модель конечных смесей с распределением Дирихле.

Используя распределение Дирихле, мы можем построить Модель конечной смеси которые можно использовать для кластеризации. Предположим, что у нас есть следующая модель:

Уравнение 3: Модель конечной смеси с распределением Дирихле

Приведенная выше модель предполагает следующее: у нас есть набор данных X с n наблюдениями, и мы хотим выполнить для него кластерный анализ. k — это постоянное конечное число, которое показывает количество кластеров/компонентов, которые мы будем использовать. с_я переменные хранят кластерное назначение наблюдения X_я, они принимают значения от 1 до k и следуют дискретному распределению с параметром p, который представляет собой вероятность смеси компонентов. F – это генеративное распределение нашего X, и оно параметризовано параметром который зависит от назначения кластера каждого наблюдения. Всего имеем k уникальных параметры равны количеству наших кластеров. переменная хранит параметры, которые параметризуют генеративное F-распределение, и мы предполагаем, что оно следует базе G₀ распределение. Переменная p хранит процентное содержание смеси для каждого из k кластеров и соответствует Дирихле с параметрами α/k. Наконец, α есть размерный вектор с гиперпараметрами (псевдоотсчетами) распределения Дирихле (2).

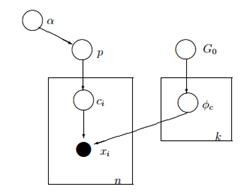
Рисунок 4: Графическая модель модели конечной смеси с распределением Дирихле

Более простой и менее математический способ объяснить модель заключается в следующем. Мы предполагаем, что наши данные можно сгруппировать в k кластеров. Каждый кластер имеет свои параметры и эти параметры используются для генерации наших данных. Параметры предполагается, что они следуют некоторому распределению G₀. Каждое наблюдение представлено вектором x_я и переменный ток_я значение, которое указывает кластер, к которому он принадлежит. Следовательно, с_я можно рассматривать как переменную, которая следует дискретному распределению с параметром p, который представляет собой не что иное, как смешанные вероятности, то есть вероятность появления каждого кластера. Учитывая, что мы решаем нашу проблему байесовским способом, мы не рассматриваем параметр p как постоянный неизвестный вектор. Вместо этого мы предполагаем, что P следует Дирихле, который параметризуется гиперпараметрами α/k.

5. Работа с бесконечными k кластерами

Предыдущая смешанная модель позволяет нам выполнять обучение без учителя, следует байесовскому подходу и может быть расширена до иерархической структуры. Тем не менее, это конечная модель, поскольку она использует постоянное заранее заданное количество кластеров k. В результате от нас требуется определить количество компонентов перед выполнением кластерного анализа, и, как мы обсуждали ранее, в большинстве приложений это неизвестно и не может быть легко оценено.

Один из способов решить эту проблему — представить, что k имеет очень большое значение, стремящееся к бесконечности. Другими словами, мы можем представить предел этой модели, когда k стремится к бесконечности. Если это так, то мы можем видеть, что, несмотря на то, что количество кластеров k бесконечно, фактическое количество активных кластеров (тех, которые имеют хотя бы одно наблюдение) не может быть больше, чем n (что равно общее количество наблюдений в нашем наборе данных). На самом деле, как мы увидим позже, количество активных кластеров будет значительно меньше, чем n, и они будут пропорциональны .

Конечно, ограничение k до бесконечности нетривиально. Возникает несколько вопросов, например, можно ли взять такой предел, как будет выглядеть эта модель и как мы можем построить и использовать такую ​​модель.

В следующей статье мы сосредоточимся именно на этих вопросах: мы дадим определение процессу Дирихле, представим различные представления ДП и, наконец, сосредоточимся на процессе китайского ресторана, который является интуитивно понятным и эффективным способом построения процесса Дирихле.

Я надеюсь, что вы нашли этот пост полезным. Если вы это сделали, пожалуйста, найдите время, чтобы поделиться статьей на Facebook и Twitter. 🙂