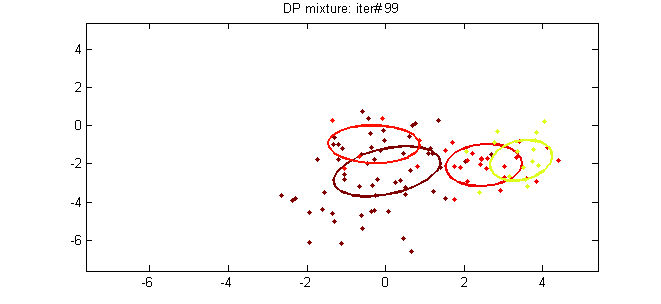
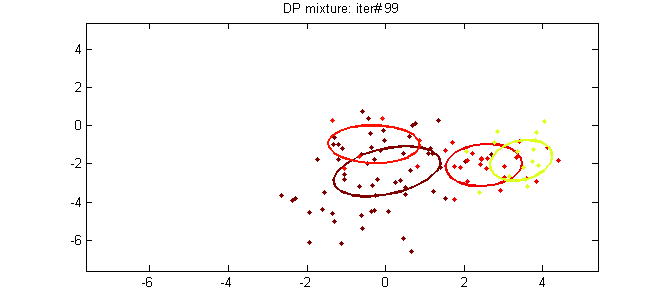Эта статья является пятой частью руководства по кластеризации с помощью DPMM. В предыдущих сообщениях мы подробно рассмотрели теоретические основы метода и описали его математические представления и способы его построения. В этом посте мы попытаемся связать теорию с практикой, представив две модели DPMM: модель многомерной нормальной смеси Дирихле, которую можно использовать для кластеризации гауссовых данных, и модель полиномиальной смеси Дирихле, которая используется для кластеризации документов.

Обновление: платформа машинного обучения Datumbox теперь имеет открытый исходный код и бесплатна для скачать. Ознакомьтесь с пакетом com.datumbox.framework.machinelearning.clustering, чтобы увидеть реализацию смешанных моделей процессов Дирихле в Java.

1. Модель многомерной нормальной смеси Дирихле.

Первая смешанная модель процесса Дирихле, которую мы рассмотрим, — это многомерная нормальная смешанная модель Дирихле, которую можно использовать для кластеризации непрерывных наборов данных. Модель смеси определяется следующим образом:

Уравнение 1: Многомерная нормальная модель смеси Дирихле

Как мы видим выше, конкретная модель предполагает, что генеративное распределение является полиномиальным распределением Гаусса, и использует процесс китайского ресторана в качестве предшествующего для кластерных назначений. Кроме того, для базового распределения G₀ он использует априорный вариант Normal-Inverse-Wishart, который сопряженный предшествующий многомерного нормального распределения с неизвестным средним значением и ковариационной матрицей. Ниже мы представляем графическую модель модели смеси:

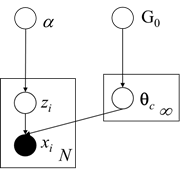
Рисунок 1: Графическая модель многомерной нормальной модели смеси Дирихле

Как мы обсуждали ранее, чтобы иметь возможность оценить кластерные назначения, мы будем использовать Свернутая выборка Гиббса который требует выбора соответствующие сопряженные априоры. Кроме того, нам нужно будет обновить параметры апостериорно предыстория и доказательства. Ниже мы видим оценки MAP параметров для одного из кластеров:

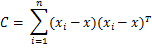
Уравнение 2: оценки MAP по параметрам кластера

Где d – размерность наших данных и является выборочным средним. Кроме того, у нас есть несколько гиперпараметров нормального обратного Вишарта, таких как μ₀ что является начальным средним значением, κ₀ – средняя доля, которая работает как параметр сглаживания, ν₀ – это степени свободы, которые задаются числом измерений и Ψ₀ представляет собой произведение попарного отклонения, которое задается единичной матрицей dxd, умноженной на константу. С этого момента все предыдущие гиперпараметры G₀ будем обозначать через λ для упрощения записи. Наконец, имея все вышеперечисленное, мы можем оценить вероятности, которые требуются для свернутого пробоотборника Гиббса. Вероятность того, что наблюдение i принадлежит кластеру k, учитывая назначения кластера, набор данных и все гиперпараметры α и λ DP и G₀ приведен ниже:

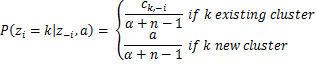
Уравнение 3: Вероятности, используемые пробоотборником Гиббса для MNMM

Где г_я кластерное назначение наблюдения x_яИкс_1:н полный набор данных, z_-я это набор кластерных назначений без одного из i^й наблюдение, х_-я полный набор данных, за исключением i^й наблюдение, с_к,-я – общее количество наблюдений, отнесенных к кластеру k, исключая i^й наблюдение в то время как и – среднее значение и ковариационная матрица кластера k, исключая i^й наблюдение.

2. Модель полиномиальной смеси Дирихле.

Модель полиномиальной смеси Дирихле используется для выполнения кластерного анализа документов. Конкретная модель имеет несколько более сложную иерархию, поскольку она моделирует темы/категории документов, вероятности слов в каждой теме, назначения кластеров и генеративное распределение документов. Его целью является выполнение обучения без учителя и кластеризация списка документов путем их распределения по группам. Модель смеси определяется следующим образом:

Уравнение 4: Модель полиномиальной смеси Дирихле

Где φ моделирует тематические вероятности, z_я селектор темы, θ_к вероятности слов в каждом кластере и x_{я, дж} представляет слова документа. Следует отметить, что этот метод использует структуру мешка слов, которая представляет документы как неупорядоченный набор слов, игнорируя грамматику и порядок слов. Это упрощенное представление обычно используется при обработке естественного языка и поиске информации. Ниже мы представляем графическую модель модели смеси:

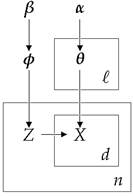
Рисунок 2: Графическая модель полиномиальной модели смеси Дирихле.

В конкретной модели используется Полиномиальное дискретное распределение для порождающего распределения и распределения Дирихле для априоров. ℓ — это размер наших активных кластеров, n — общее количество документов, β управляет априорно ожидаемым количеством кластеров, а α управляет количеством слов, назначенных каждому кластеру. Для оценки вероятностей, необходимых для Свернутый пробоотборник Гиббса мы используем следующее уравнение:

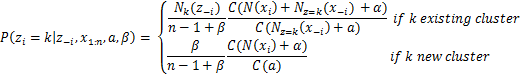
Уравнение 5: Вероятности, используемые пробоотборником Гиббса для DMMM

Где Γ — гамма-функция, z_я кластерное назначение документа x_яИкс_1:н полный набор данных, z_-я это набор кластерных назначений без одного из i^й документ, х_-я полный набор данных, за исключением i^й документ, Н_к(г_-я) — количество наблюдений, отнесенных к кластеру k, исключая i^й документ, Н_г=к(Икс_-я) представляет собой вектор с суммами отсчетов для каждого слова для всех документов, относящихся к кластеру k, исключая i^й документ и N(x_я) — разреженный вектор с количеством каждого слова в документе x_я. Наконец, как мы можем видеть выше, используя Collapsed Gibbs Sampler с китайским рестораном, обработайте θ_Джейк переменная, которая хранит вероятность слова j в теме k, может быть проинтегрирована.