Глубокие нейронные сети сделали возможными технологические чудеса, начиная от распознавания голоса и заканчивая машинным переходом к белковой инженерии, но их дизайн и применение, тем не менее, заведомо беспринципны. Разработка инструментов и методов для управления этим процессом — одна из главных задач теории глубокого обучения. В Реверс-инжиниринг ядра нейронной касательной, мы предлагаем парадигму привнесения некоторых принципов в искусство архитектурного проектирования с использованием недавних теоретических открытий: сначала спроектируйте хорошую функцию ядра — часто гораздо более легкую задачу — а затем «обратно спроектируйте» сетевую эквивалентность ядра, чтобы транслировать выбранное ядро. в нейронную сеть. Наш основной теоретический результат позволяет разрабатывать функции активации из первых принципов, и мы используем его для создания одной функции активации, которая имитирует производительность глубокой \(\textrm{ReLU}\) сети только с одним скрытым слоем, а другой значительно превосходит глубокую \( \textrm{ReLU}\) сетей на синтетической задаче.

Ядра обратно в сети. Основополагающие работы вывели формулы, которые отображают широкие нейронные сети в соответствующие им ядра. Мы получаем обратное отображение, позволяющее нам начать с желаемого ядра и превратить его обратно в сетевую архитектуру.

Ядра нейронной сети

Область теории глубокого обучения недавно была преобразована осознанием того, что глубокие нейронные сети часто становятся аналитически поддающимися изучению в реальном времени. бесконечная ширина предел. Примите ограничение определенным образом, и сеть фактически сходится к обычному методу ядра, используя либо архитектурные «нейронное касательное ядро» (NTK) или, если обучается только последний слой (как модели случайных признаков), его Ядро «нейронной сети Гауссовский процесс» (NNGP). Как и центральная предельная теорема, эти ограничения для широкой сети часто являются удивительно хорошими приближениями даже вдали от бесконечной ширины (часто остаются верными при ширине в сотни или тысячи), что дает замечательный аналитический подход к тайнам глубокого обучения.

От сетей к ядрам и обратно

Первоначальные работы, исследующие это соответствие сетевого ядра, дали формулы для перехода от архитектура к ядро: учитывая описание архитектуры (например, глубину и функцию активации), они дают вам два ядра сети. Это позволило лучше понять оптимизацию и обобщение различных интересующих архитектур. Однако если наша цель состоит не только в том, чтобы понять существующие архитектуры, но и в том, чтобы спроектировать новый единицы, то мы могли бы скорее иметь отображение в обратном направлении: учитывая ядро мы хотим, можем ли мы найти архитектура что дает это нам? В этой работе мы получаем это обратное отображение для полносвязных сетей (FCN), что позволяет нам проектировать простые сети принципиальным образом, (а) устанавливая желаемое ядро ​​и (б) разрабатывая функцию активации, которая его дает.

Чтобы понять, почему это имеет смысл, давайте сначала визуализируем NTK. Рассмотрим NTK широкого FCN \(K(x_1,x_2)\) на двух входных векторах \(x_1\) и \(x_2\) (которые мы будем для простоты считать нормированными к одинаковой длине). Для FCN это ядро инвариантный к вращению в том смысле, что \(K(x_1,x_2) = K(c)\), где \(c\) – косинус угла между входами. Поскольку \(K(c)\) является скалярной функцией скалярного аргумента, мы можем просто построить ее график. На рис. 2 показана NTK четырехслойной (4HL) \(\textrm{ReLU}\) FCN.

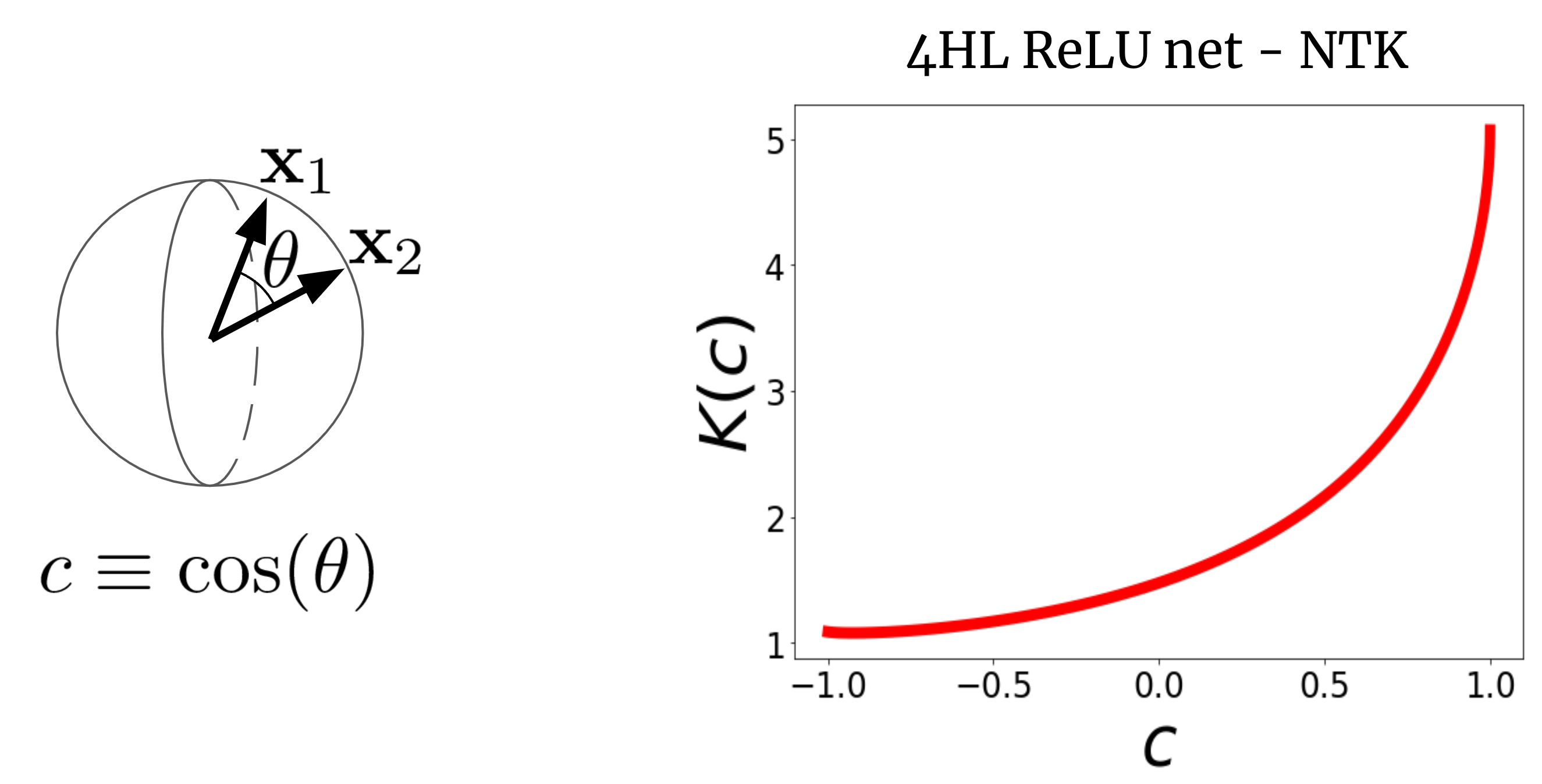
Рис 2. NTK 4HL $\textrm{ReLU}$ FCN как функция косинуса между двумя входными векторами $x_1$ и $x_2$.

Этот график на самом деле содержит много информации об обучающем поведении соответствующей широкой сети! Монотонное увеличение означает, что это ядро ​​​​предполагает, что более близкие точки будут иметь более коррелированные значения функции. Крутой рост в конце говорит нам о том, что длина корреляции не слишком велика и может соответствовать сложным функциям. Расходящаяся производная в точке \(c=1\) говорит нам о гладкости функции, которую мы ожидаем получить. Важно, ни один из этих фактов не очевиден при взгляде на график \(\textrm{ReLU}(z)\)! Мы утверждаем, что если мы хотим понять эффект выбора функции активации \(\phi\), то результирующий NTK на самом деле более информативен, чем сам \(\phi\). Таким образом, возможно, имеет смысл попытаться спроектировать архитектуру в «пространстве ядра», а затем преобразовать ее в типичные гиперпараметры.

Функция активации для каждого ядра

Наш основной результат — «теорема обратного проектирования», которая утверждает следующее:

Тема 1: Для любого ядра $K(c)$ можно построить функцию активации $\tilde{\phi}$ такую, что при вставке в однослойный скрытый слой FCN, его ядро ​​NTK или NNGP бесконечной ширины равно $K(c)$.

Мы даем явную формулу для \(\tilde{\phi}\) в терминах полиномов Эрмита (хотя на практике мы используем другую функциональную форму из соображений обучаемости). Предлагаемое нами использование этого результата заключается в том, что в задачах с некоторой известной структурой иногда можно записать хорошее ядро ​​и реконструировать его в обучаемую сеть с различными преимуществами по сравнению с чистой регрессией ядра, такими как вычислительная эффективность и производительность. способность изучать особенности. В качестве доказательства концепции мы тестируем эту идею на синтетическом проблема четности (т. е. если задана битовая строка, является ли сумма нечетной или четной?), немедленно генерируя функцию активации, которая значительно превосходит \(\text{ReLU}\) в задаче.

Один скрытый слой — это все, что вам нужно?

Вот еще одно неожиданное использование нашего результата. Приведенная выше кривая ядра предназначена для 4HL \(\textrm{ReLU}\) FCN, но я утверждал, что мы можем получить любое ядро, включая это, всего с одним скрытым слоем. Это означает, что мы можем придумать новую функцию активации \(\tilde{\phi}\), которая дает этот «глубокий» NTK в мелкая сеть! Рис. 3 иллюстрирует этот эксперимент.

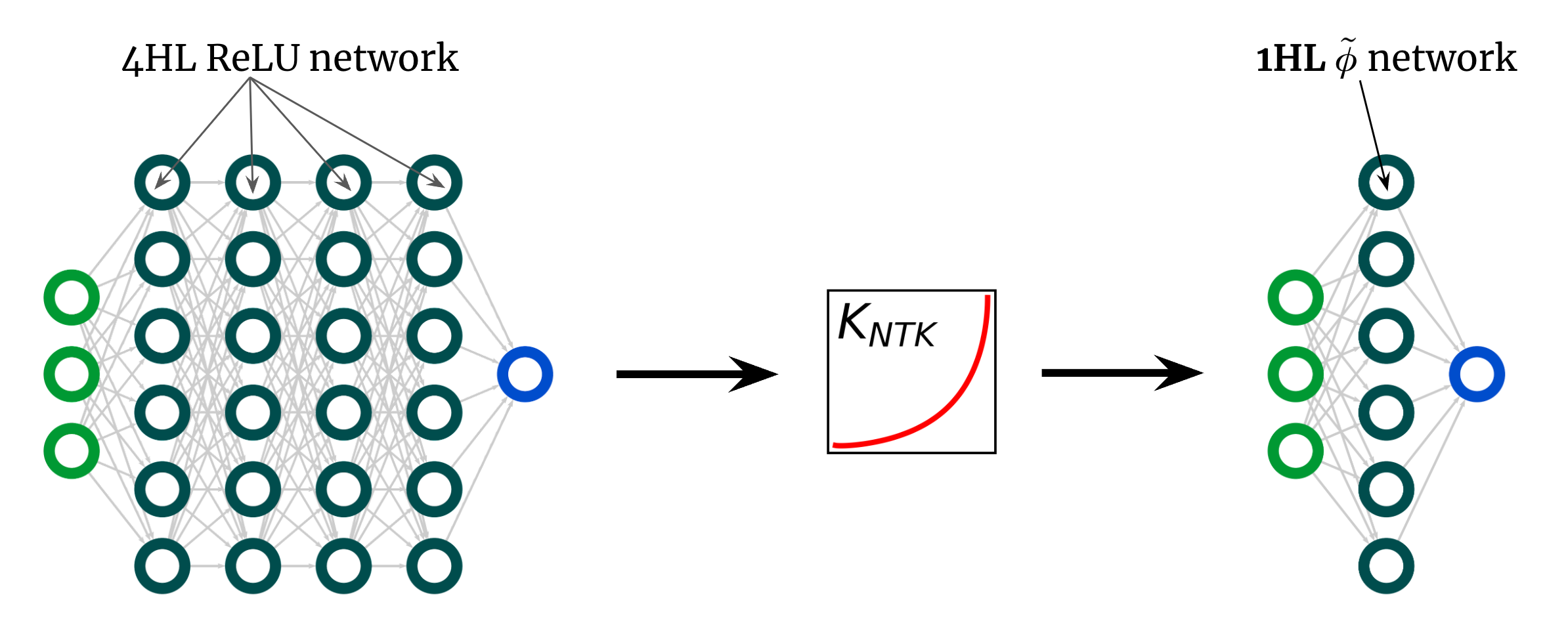
Рис 3. Преобразование глубокого $\textrm{ReLU}$ FCN в 1HL FCN с инженерной функцией активации $\tilde{\phi}$.

Удивительно, но эта «поверхностность» действительно работает. Левый подграфик на рис. 4 ниже показывает «имитирующую» функцию активации \(\tilde{\phi}\), которая дает практически тот же NTK, что и глубокий \(\textrm{ReLU}\) FCN. Затем правые графики показывают поезд + потери при тестировании + трассировки точности для трех FCN в стандартной табличной задаче из набора данных UCI. Обратите внимание, что хотя поверхностная и глубокая сети ReLU имеют очень разное поведение, наша спроектированная поверхностная имитирующая сеть почти точно отслеживает глубокую сеть!

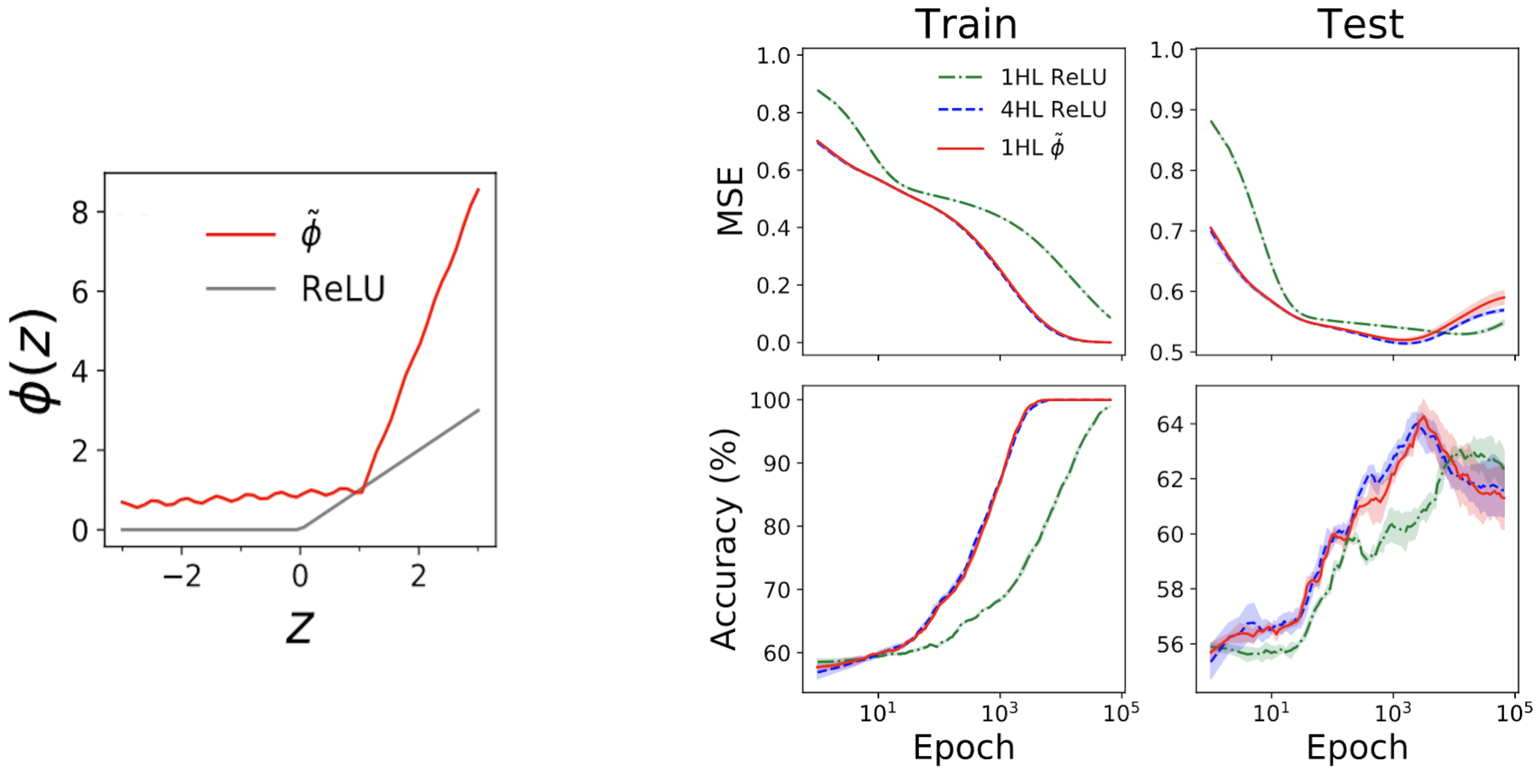
Рис 4. Левая панель: наша инженерная «имитирующая» функция активации, построенная с помощью ReLU для сравнения. Правые панели: трассировки производительности для 1HL ReLU, 4HL ReLU и 1HL имитирующих FCN, обученных на наборе данных UCI. Обратите внимание на близкое соответствие между имитационными сетями 4HL ReLU и 1HL.

Это интересно с инженерной точки зрения, поскольку неглубокая сеть использует меньше параметров, чем глубокая сеть, для достижения той же производительности. Это также интересно с теоретической точки зрения, потому что поднимает фундаментальные вопросы о значении глубины. Распространенным убеждением в глубоком обучении является то, что глубже не только лучше, но и лучше. качественно разные: что глубокие сети будут эффективно изучать функции, которые мелкие сети просто не могут. Наш результат измельчения предполагает, что, по крайней мере для FCN, это неверно: если мы знаем, что делаем, то глубина нам ничего не даст.

Заключение

Эта работа имеет много предостережений. Самый большой из них заключается в том, что наш результат применим только к FCN, которые сами по себе редко бывают современными. Однако работа над сверточными НТК быстро прогрессируети мы считаем, что эта парадигма проектирования сетей путем проектирования ядер созрела для расширения в той или иной форме на эти структурированные архитектуры.

Теоретическая работа до сих пор предоставила относительно мало инструментов для практических теоретиков глубокого обучения. Мы стремимся к тому, чтобы это был скромный шаг в этом направлении. Даже без науки, управляющей их дизайном, нейронные сети уже творят чудеса. Только представьте, что мы сможем с ними сделать, когда они у нас наконец появятся.

Этот пост основан на бумага «Обратный инжиниринг нейронного касательного ядра», который является совместной работой с Саджант Ананд и Майк ДеВиз. Мы предоставляем код чтобы воспроизвести все наши результаты. Мы будем рады ответить на ваши вопросы или комментарии.