На этот раз мы собираемся занять себя другим семейством алгоритмов обучения с подкреплением, называемых методами, основанными на политике. Если вы помните, есть две основные группы методов обучения с подкреплением без использования моделей.

Мы анализируем первые в двух предыдущих статьях, где мы говорили о Q-learning и Deep Q Networks, а также о различных улучшениях базовых моделей, таких как Double Deep Q Networks и Prioritized Replay. Посмотрите их здесь и здесь.

Давайте сделаем быструю перемотку. Помните, что мы формулируем наши проблемы как марковские процессы принятия решений и что наша цель — найти наилучшую политику, которая представляет собой отображение состояний в действия. Другими словами, мы хотим знать, каково действие с максимальным ожидаемым вознаграждением в данном состоянии. В методах, основанных на значениях, мы достигаем этого, находя или аппроксимируя функцию значения, а затем извлекая политику. Что, если мы полностью отбросим ценностную часть и найдем непосредственно Политику. Это то, что делают методы, основанные на политике.

Не поймите меня неправильно. Сети Q-learning и Deep Q великолепны, и они используются во многих приложениях, но методы, основанные на политике, предлагают несколько других преимуществ:

• Они легче сходятся к локальному или глобальному максимуму и не подвержены осцилляциям.

• Они очень эффективны в многомерных или непрерывный пространства

• Они могут учиться стохастический политики (стохастические политики дают
  распределение вероятностей действия, а не детерминированное действие. Они использовали в стохастических средах, которые они смоделировали как частично наблюдаемые марковские процессы принятия решений, где мы точно не знаем результат каждого действия)

Подожди минутку. Я говорил о сходимости, локальном максимуме, непрерывном пространстве, стохастичности. Что здесь происходит?

Ну, дело в том, что Обучение с подкреплением, основанное на политике, является проблемой оптимизации. Но что это значит?

У нас есть политика (π) с некоторыми параметрами тета (θ), которая выводит распределение вероятностей по действиям. Мы хотим найти наилучшую тету, которая производит наилучшую политику. Но как мы оцениваем, хороша политика или плоха? Мы используем целевую функцию политики J(θ), которая чаще всего представляет собой ожидаемое накопительное вознаграждение. Кроме того, целевая функция различается в зависимости от того, имеем ли мы эпизодическую или продолжающуюся среду.

Итак, мы здесь, с проблемой оптимизации в наших руках. Все, что нам нужно сделать, это найти параметры тета (θ), которые максимизируют J (θ), и у нас есть оптимальная политика.

Первый подход заключается в использовании метода грубой силы и проверке всего пространства политики. Хм, не так хорошо.

Второй подход заключается в использовании прямого поиска в пространстве политик или его подмножестве. И здесь мы вводим термин Поиск политики. На самом деле есть два семейства алгоритмов, которые мы можем использовать. Назовем их:

• Градиент бесплатно

• Градиент на основе

Подумайте о любом алгоритме, который вы когда-либо использовали для решения задачи оптимизации, в котором не используются производные. Это безградиентный метод, и большинство из них можно использовать в нашем случае. Вот некоторые примеры:

• скалолазание это случайный итеративный локальный поиск

• Симплекс: популярный алгоритм линейного программирования (если вы копаетесь в линейной алгебре, посмотрите его)

• Имитация отжигакоторый перемещается по разным состояниям на основе некоторой вероятности.

• Эволюционные алгоритмы которые моделируют процесс физической эволюции. Они начинают со случайного состояния, представленного в виде генома, и путем скрещивания, мутации и физического отбора находят самое сильное поколение (или максимальное значение). Вся концепция «Выживает сильнейший», заключенная в алгоритм.

Второе семейство методов использует Градиентный спуск или, если быть более точным, градиентное восхождение.

В (ванильном) градиентном спуске мы:

1. Инициализировать параметры тета

2. Создать следующий эпизод

3. Получите долгосрочное вознаграждение

4. Обновить тета на основе вознаграждения за все временные шаги

5. Повторить

Но есть небольшая проблема. Можем ли мы вычислить градиент тета в аналитической форме? Потому что, если мы не сможем, весь процесс пойдет в мусорку. Оказывается, мы можем с небольшой хитростью. Мы должны предположить, что политика дифференцируема, когда она отлична от нуля, и использовать логарифмы. Кроме того, мы определяем траекторию состояния-действия (τ) как последовательность состояний, действий и наград: τ = (s0,a0,r0, s1,a1,r1…, st,at,rt).

Я думаю, что достаточно математики для одного дня. В результате, конечно же, у нас есть градиент в аналитической форме, и теперь мы можем применить наш алгоритм.

Алгоритм, описанный до сих пор (с небольшой разницей), называется
УКРЕПИТЬ или Градиент политики Монте-Карло. Отличие от градиентов ванильной политики в том, что мы избавились от ожидания в награде, так как это не очень практично. Вместо этого мы используем стохастический градиентный спуск для обновления тета. Мы образец от ожидания рассчитать вознаграждение за эпизод и затем обновить параметры для каждого шага эпизода. Это довольно простой алгоритм.

Хорошо, давайте упростим все эти вещи. Вы можете думать о градиентах политики так:

Для каждого эпизода, в котором мы получили положительное вознаграждение, алгоритм будет увеличивать вероятность этих действий в будущем. Точно так же для отрицательных вознаграждений алгоритмы уменьшат вероятность действий. В результате со временем действия, приводящие к отрицательным результатам, будут постепенно отфильтровываться, а действия с положительными результатами будут становиться все более и более вероятными. Вот и все. Если вы хотите запомнить что-то одно из всей статьи, то это оно. В этом суть градиентов политики. Единственное, что каждый раз меняется, это то, как мы вычисляем вознаграждение, какую политику выбираем (Softmax, Gaussian и т. д.) и как мы обновляем параметры.

Теперь давайте двигаться дальше.

REINFORCE, как уже упоминалось, является алгоритмом стохастического градиентного спуска. Учитывая это, возникает вопрос. Почему бы не использовать нейронные сети для аппроксимации политики и обновления тета?

Бинго!!

Пришло время ввести в уравнение нейронные сети:

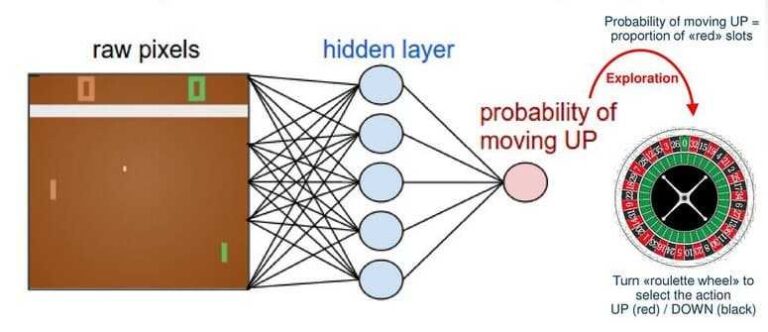
Конечно, мы можем использовать практически любую модель машинного обучения для аппроксимации функции политики (π), но мы используем нейронную сеть, такую ​​как сверточная сеть, потому что нам нравится глубокое обучение. Известный пример — агент, который учится играть в игру понг используя градиенты политик и нейронные сети. В этом примере сеть получает в качестве входных данных кадры из игры и выводит вероятность повышения или понижения.

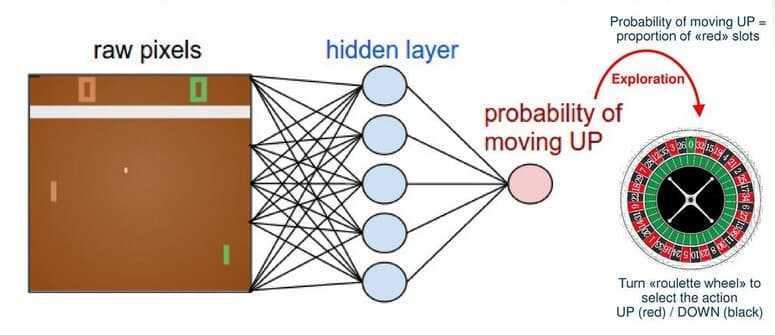
http://karpathy.github.io/2016/05/31/rl/

Мы попробуем сделать что-то подобное, используя тренажерный зал. OpenAI.

class REINFORCEAgent:
    def build_model(self):
        model = Sequential()
        model.add(Dense(self.hidden1, input_dim=self.state_size, activation='relu', kernel_initializer='glorot_uniform'))
        model.add(Dense(self.hidden2, activation='relu', kernel_initializer='glorot_uniform'))
        model.add(Dense(self.action_size, activation='softmax', kernel_initializer='glorot_uniform'))
        model.compile(loss="categorical_crossentropy", optimizer=Adam(lr=self.learning_rate))
        return model
    def get_action(self, state):
        policy = self.model.predict(state, batch_size=1).flatten()
        return np.random.choice(self.action_size, 1, p=policy)(0)
    def discount_rewards(self, rewards):
        discounted_rewards = np.zeros_like(rewards)
        running_add = 0
        for t in reversed(range(0, len(rewards))):
            running_add = running_add * self.discount_factor + rewards(t)
            discounted_rewards(t) = running_add
        return discounted_rewards
    def train_model(self):
        episode_length = len(self.states)
        discounted_rewards = self.discount_rewards(self.rewards)
        discounted_rewards -= np.mean(discounted_rewards)
        discounted_rewards /= np.std(discounted_rewards)
        update_inputs = np.zeros((episode_length, self.state_size))
        advantages = np.zeros((episode_length, self.action_size))
        for i in range(episode_length):
            update_inputs(i) = self.states(i)
            advantages(i)(self.actions(i)) = discounted_rewards(i)
        self.model.fit(update_inputs, advantages, epochs=1, verbose=0)
env = gym.make('CartPole-v1')
state_size = env.observation_space.shape(0)
action_size = env.action_space.n
scores, episodes = (), ()
agent = REINFORCEAgent(state_size, action_size)
for e in range(EPISODES):
    done = False
    score = 0
    state = env.reset()
    state = np.reshape(state, (1, state_size))
    while not done:
        if agent.render:
            env.render()
        action = agent.get_action(state)
        next_state, reward, done, info = env.step(action)
        next_state = np.reshape(next_state, (1, state_size))
        reward = reward if not done or score == 499 else -100
        agent.append_sample(state, action, reward)
        score += reward
        state = next_state
        if done:
            agent.train_model()
            score = score if score == 500 else score + 100
            scores.append(score)
            episodes.append(e)

Вы можете видеть, что это не тривиально. Мы определяем модель нейронной сети, выборку Монте-Карло, процесс обучения, а затем позволяем агенту учиться, взаимодействуя с окружающей средой, и обновляем вес в конце каждого эпизода.

Для получения дополнительных материалов о градиентах политики я настоятельно рекомендую Продвинутый ИИ: курс глубокого обучения на Python на Удеми. Он охватывает все, что вам нужно знать, от Deep Q Learning до градиентов политики и критики актеров.

Но градиенты политики имеют свои недостатки. Наиболее важным является то, что они имеют высокую дисперсию, и стабилизировать параметры модели может быть очень сложно.

Хочешь знать, как мы это решим? Поддерживать связь…

(Подсказка: его модели актеров-критиков)

Книга «Глубокое обучение в производстве» 📖

Узнайте, как создавать, обучать, развертывать, масштабировать и поддерживать модели глубокого обучения. Изучите инфраструктуру машинного обучения и MLOps на практических примерах.

Узнать больше

* Раскрытие информации: Обратите внимание, что некоторые из приведенных выше ссылок могут быть партнерскими ссылками, и без дополнительной оплаты для вас мы будем получать комиссию, если вы решите совершить покупку после перехода по ссылке.