Этот пост был первоначально опубликован мной на Блог Фортскейла.
Продукт Fortscale помогает организациям устранять внутренние угрозы, обнаруживая аномальное поведение пользователей.

В предыдущем посте этой серии я описал, как мы в Fortscale используем персонализированный адаптивный порог для запуска предупреждений. Каждому действию пользователя присваивается оценка риска (известная как значение SMART), которая вызывает оповещение SMART при пересечении порога пользователя. Мы объяснили, что чем больше аномальных действий совершает пользователь с течением времени, тем выше становится его порог. Это создает желаемый эффект, заключающийся в том, что аналитик будет уведомлен о пользователе только тогда, когда этот пользователь выполняет действительно аномальную деятельность, даже для него самого.

Более того, мы объяснили, почему и как мы включаем аномальную активность всей организации в порог пользователя, чтобы аналитика не беспокоили предупреждения от пользователей, которые являются аномальными, но недостаточно аномальными по сравнению с другими пользователями.

В этом посте я подробно расскажу о том, как мы реализовали SMART-подход. В частности, я опишу структуру байесовского вывода и подробно расскажу о том, как мы использовали ее для создания персонализированного адаптивного пользовательского порога.

Байесовский вывод — это метод расчета вероятностей. Вероятность интереса в нашем случае — это вероятность того, что данный пользователь выполнит аномальное действие с относительно высоким значением SMART. Если мы сможем оценить эту вероятность, мы сможем использовать ее для присвоения соответствующей оценки каждому действию.

Возьмем, к примеру, Джо. Джо никогда не совершал каких-либо радикальных аномальных действий. Он сгенерировал значения SMART в основном в диапазоне от 0,1 до 0,2. Создание значения SMART 0,6 для него очень маловероятно. Допустим, мы оцениваем, что вероятность того, что Джо сгенерирует значение SMART, равное 0,6, составляет всего 1%. Если Джо сгенерирует значение SMART, равное 0,6, мы сможем использовать эту вероятность и присвоить этому действию оценку риска 99 (что равно 100 минус вероятность). Мы могли бы решить, что только оценки риска выше некоторого порога (например, 95) должны вызывать оповещение. В этом посте мы предположим некоторый предварительно настроенный порог, но будьте готовы, выбор правильного порога также является сложной задачей. Мы опишем методы, которые мы используем для расчета этого порога, в отдельном посте.

Чтобы рассчитать вероятность, нам сначала нужно смоделировать наши данные. Давайте визуализируем значения SMART, собранные для всех пользователей организации у одного из наших клиентов:

Поскольку большинство значений SMART равны нулю, что имеет смысл, поскольку большую часть времени пользователи не совершают аномальных действий, эту гистограмму трудно интерпретировать… Давайте проверим те же данные, отбросив все нули:

Так-то лучше. Теперь мы можем увидеть две закономерности в данных:

1. Высокие значения SMART встречаются реже, чем низкие.
2. Кажется, что частота затухает агрессивно (убывает быстрее линейного темпа).

Позволять \(В\) быть случайной переменной, представляющей значение SMART, которое может иметь пользователь. Естественным выбором модели было бы экспоненциальное распределение (для некоторых \(\лямбда\) который является параметром модели):

$$Prob(\text{V = v}) = \lambda e^{-\lambda v}$$

Мы могли бы проверить, что эта модель имеет хороший соответствие, но нам это и не нужно; мы должны помнить, что наша цель — дать высокие баллы пользователям, которые выполняют действия, которые являются чрезвычайно аномальными по сравнению с их собственной моделью поведения. Мы могли бы выбрать другие модели, которые могут описывать данные, например модель с обратной пропорциональной зависимостью, но по сравнению с экспоненциальной моделью это дало бы более низкие баллы для исключительно высоких значений SMART. Мы выбрали более агрессивную экспоненциальную модель, потому что она лучше снижает количество ложных срабатываний.

Поскольку мы моделируем каждого пользователя отдельно, мы должны исследовать и убедиться, что данные каждого пользователя следуют одной и той же схеме более или менее экспоненциального затухания; и это так.

Чтобы иметь возможность вычислить вероятности для Джо, нам сначала нужно оценить его модель. \(\лямбда\) от его прошлых значений SMART. Один частотный подход будет использовать оценку максимального правдоподобия (MLE) метод для оценки \(\лямбда\). Проблема с этим подходом в том, что мы получаем точечная оценка: если бы нам пришлось угадывать лучший \(\лямбда\) и у нас был только один выстрел, тогда MLE, вероятно, был бы нашим лучшим выбором. Но мы можем добиться большего успеха, используя другие методы, учитывающие неопределенности.

Чтобы лучше проиллюстрировать проблему, давайте рассмотрим более простую и понятную задачу оценки того, насколько смещена монета. Позволять \(п\) быть вероятностью подбрасывания HEAD. Тогда целью становится оценка \(п\). Если мы подбросим монету 10 раз и 3 раза выпадет ГОЛОВА, мы можем оценить \(п\) быть 0,3 с использованием MLE. Очевидно, у нас есть сомнения в этой оценке, так как данных недостаточно; может быть это \(п\) равно 0,5, и мы получили только 3 HEAD из-за случайности. Если бы мы подбросили вторую монету 1000 раз и получили 300 HEAD, MLE по-прежнему был бы равен 0,3, но на этот раз наша уверенность была бы выше.

Существует множество математических подходов, которые мы могли бы применить здесь для учета неопределенностей. Мы выбрали байесовский подход к выводу. Байесианство и частотность – два ключевых подхода, используемых для оценки вероятностей, которые представляют собой два разных философских подхода. Байесовский метод рассматривает параметр модели как случайную переменную, что означает, что он может иметь любое значение, и существует функция распределения, называемая априорной, которая может сказать нам, какие значения более вероятны, чем другие. С другой стороны, частотный подход утверждает, что параметр модели является фиксированной величиной; в этом нет ничего случайного, и никто не может утверждать свое предварительное убеждение. Приоритет Байеса пригодится, поэтому мы выбрали байесовский подход.

Давайте изучим математику. Позволять \(в\) быть некоторым гипотетическим значением SMART, которое мог бы сгенерировать Джо, и \(Данные\) быть его прошлыми значениями SMART. Мы можем использовать некоторые основные свойства вероятности, чтобы вывести следующее:

$$ \begin{split} Prob(v | Data) &= \int_{0}^{\infty} Prob(v, \lambda | Data) d\lambda \quad&\text{(1.)} \\ & = \int_{0}^{\infty} Prob(v | \lambda, Data) Prob(\lambda | Data) d\lambda \quad&\text{(2.)} \\ &= \int_{0}^ {\infty} Prob(v | \lambda) Prob(\lambda | Data) d\lambda \quad&\text{(3.)} \\ &= \int_{0}^{\infty} \lambda e^{ -\lambda v} * Prob(\lambda | Data) d\lambda \quad&\text{(4.)} \end{split} $$

Шаги уравнения

1. Используйте маргинализацию вероятности: интегрируйте по всем \(\лямбда\)возможные значения.
2. Использовать Правило цепи.
3. Используйте предположение, что значения SMART не зависят друг от друга, поэтому \(в\) не зависит от \(Данные\).
4. Замените вероятность оценкой экспоненциального распределения: \(v \sim Exp(\лямбда)\).

Единственная недостающая часть головоломки заключается в том, как оценить \(Вероятность(\лямбда | Данные)\). Байесовский подход к выводу использует правило Байеса следующим образом:

$$Prob(\lambda | Data) = \dfrac{Prob(Data | \lambda) Prob(\lambda)}{Prob(Data)}$$

Теперь нам нужно рассчитать вероятность \(Данные\) данный \(\лямбда\)а вероятность \(\лямбда\).

Первая часть проста; это функция правдоподобия. Поскольку мы предполагаем, что значения SMART независимы, мы получаем

$$ \begin{split} Prob(Data | \lambda) &= \prod_{v_i \in Data} Prob(v_i | \lambda) \\ &= \prod_{v_i \in Data} \lambda e^{-\ lambda v_i} \\ &= \lambda e^{-\lambda \sum_{v_i \in Data}v_i} \end{split} $$

Вторая часть — это Приор, который выражает наши убеждения о \(\лямбда\) до того, как будут приняты во внимание какие-либо доказательства. Оказывается, если мы выберем конкретную априорную функцию, мы выиграем хорошее свойство, где можно аналитически вычислить \(Вероятность(\лямбда | Данные)\). С точки зрения реализации это означает, что мы можем написать его в красивой закрытой форме без необходимости выполнять утомительные вычисления или использовать численные методы во время выполнения. Я не буду утомлять вас подробностями, но в случае экспоненциальной модели, если вы выберете Prior, чтобы иметь гамма-распределение, то \(Вероятность(\лямбда | Данные)\) (также известный как Задний план) также является Гаммой с обновленными параметрами. Этот вид Prior известен как сопряженный предшествующий.

Гамма-распределение имеет два параметра, определяющих его форму: \(\альфа\) и \(\бета\). Допустим, мы выбираем \(\alpha_{предыдущий}\) и \(\бета_{предыдущий}\) для приора. Эти параметры заявляют о нашей вере в значения \(\лямбда\) могу взять. Как только мы наблюдаем некоторые SMART-значения пользователя, мы обновляем наше априорное убеждение и получаем апостериорную, которая представляет собой гамму с параметрами \(\alpha_{предыдущий} + N\) (где \(Н\) количество значений SMART) и \(\beta_{preor} + \sum_{v_i \in \{\text{значения SMART пользователя}\}}v_i\).

Если мы включим его в наши расчеты \(Вероятность (v | Данные)\)и после утомительных вычислений, которые мы избавим от читателя, получим

$$ \begin{split} Prob(v | Data) &= \int_{0}^{\infty} \lambda e^{-\lambda v} * Prob(\lambda | Data) d\lambda \\ &= \quad … \quad \\ &= \dfrac{\alpha_{приор} + n}{\beta_{приор} + \sum_{i=1}^{n} v_i + v} \left(\dfrac{ \beta_{предыдущий} + \sum_{i=1}^{n} v_i}{\beta_{предыдущий} + \sum_{i=1}^{n} v_i + v}\right)^{\alpha_{предыдущий } + п} \end{split} $$

Поскольку значения SMART непрерывны, мы не должны вычислять \(Вероятность (V = v | Данные)\). Вместо этого мы должны вычислить \(Prob(V \geq v | Данные)\)то есть (после интегрирования)

$$\left(\dfrac{\beta_{preor} + \sum_{i=1}^{n} v_i}{\beta_{prior} + \sum_{i=1}^{n} v_i + v}\ справа) ^ {\ alpha_ {предыдущий} + n} $ $

На данный момент у нас есть хорошая формула для вероятности увидеть значение SMART не ниже \(в\). Эта формула имеет два входа: персональные данные пользователя и Приор. Чем выше значения SMART у пользователя, тем выше вероятность увидеть \(в\) получает, что, следовательно, означает более низкую оценку риска. Если у пользователя слишком много аномалий, оценка риска \(в\) триггеры ниже установленного нами порога, и оповещение не будет создано. Мы видим адаптивный порог в действии! Хороший…

Вот пример гистограммы прошлых значений SMART конкретного пользователя:

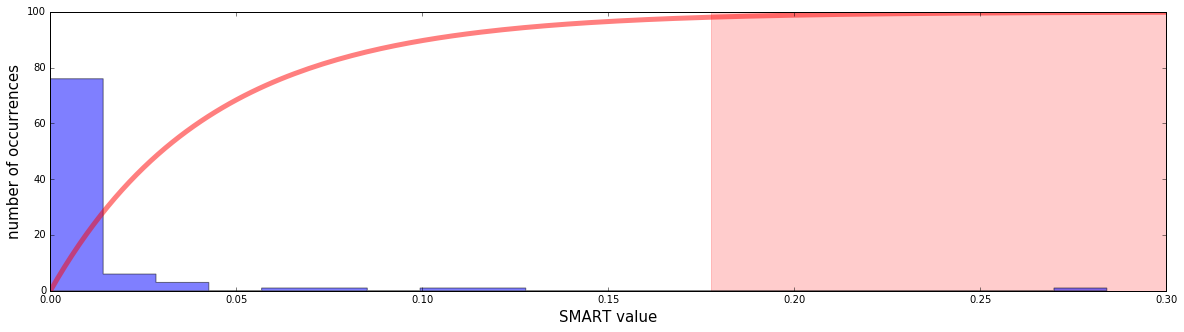
У пользователя было много значений SMART, близких к нулю, и несколько высоких. Самый высокий из них совершенно исключительный, около 0,28. Красная кривая — это функция оценки (единица минус вышеупомянутая вероятность, умноженная на 100). Светло-красная область — это область, в которой количество баллов превышает 95. В этой области будут срабатывать предупреждения. Мы видим, что значение SMART 0,28 действительно вызывает предупреждение.

В следующем посте подробно расскажу как выбрать хорошую приору \(\alpha_{предыдущий}\) и \(\бета_{предыдущий}\)так что следите за обновлениями.