Это совместный пост с Инбар Наор. Первоначально опубликовано на Engineering.taboola.com.

Понимание того, чего модель не знает, важно как с точки зрения специалиста, так и для конечных пользователей многих различных приложений машинного обучения. В наш предыдущий пост в блоге мы обсудили различные типы неопределенности. Мы объяснили, как мы можем использовать его для интерпретации и отладки наших моделей.

В этом посте мы обсудим различные способы получения неопределенности в глубоких нейронных сетях. Давайте начнем с рассмотрения нейронных сетей с байесовской точки зрения.

Байесовская статистика позволяет нам делать выводы, основанные как на свидетельствах (данных), так и на наших предварительных знаниях о мире. Это часто противопоставляется частотной статистике, которая учитывает только доказательства. Априорные знания отражают наше мнение о том, какая модель сгенерировала данные или каковы веса этой модели. Мы можем представить это убеждение с помощью предварительное распределение \(р(ш)\)
над весом модели.

По мере того, как мы собираем больше данных, мы обновляем предыдущее распределение и превращаемся в
заднее распределение используя закон Байеса, в процессе, называемом байесовское обновление:

\(p(w|X,Y) = \frac{p(Y|X,w) p(w)}{p(Y|X)}\)

Это уравнение представляет еще одного ключевого игрока в байесовском обучении —
вероятностьопределяется как \(р(у|х,ш)\). Этот термин показывает, насколько вероятны данные с учетом весов модели. \(ш\).

Задача нейронной сети — оценить вероятность \(р(у|х,ш)\). Это верно, даже если вы явно этого не делаете, например когда вы минимизируете MSE.

Чтобы найти наилучшие веса моделей, мы можем использовать Оценка максимального правдоподобия (МЛЭ):

\begin{split} w^{MLE} &= \text{argmax}_{w}\text{log}P(D|w) \\ & = \text{argmax}_{w}\sum_i \text{ log}P(y_i|x_i,w) \end{split}

В качестве альтернативы мы можем использовать наши предварительные знания, представленные в виде априорного распределения по весам, и максимизировать апостериорное распределение. Этот подход называется Максимальная апостериорная оценка (КАРТА):

\begin{split} w^{MAP} &= \text{argmax}_{w}\text{log}P(w|D) \\ & = \text{argmax}_{w}\text{log} P(D|w) + \text{log}P(w) \end{split}

Термин \(\текст{журнал}P(ш)\), который представляет наш априор, действует как член регуляризации. Выбрав распределение Гаусса со средним значением 0 в качестве априорного, вы получите математическую эквивалентность регуляризации L2.

Теперь, когда мы начинаем думать о нейронных сетях как о вероятностных существах, мы можем начать самое интересное. Во-первых, кто сказал, что мы должны выводить один набор весов в конце тренировочного процесса? Что, если вместо изучения весов модели мы узнаем распределение по весам? Это позволит нам оценить неопределенность весов. Итак, как мы это делаем?

Мы снова начинаем с априорного распределения по весам и стремимся найти их апостериорное распределение. На этот раз вместо непосредственной оптимизации весов сети мы усредним все возможные веса (называемые маргинализацией).

При выводе вместо того, чтобы брать единственный набор весов, который максимизировал апостериорное распределение (или вероятность, если мы работаем с MLE), мы рассматриваем все возможные веса, взвешенные по их вероятности. Это достигается с помощью интеграла:

\ (p (y | x, X, Y) = {\ displaystyle \ int} p (y | x, w) p (w | X, Y) dw \)

\(Икс\) это точка данных, для которой мы хотим сделать вывод \(у\)и \(ИКС\),\(Д\) являются обучающими данными. Первый срок \(р(у|х,ш)\) наша старая добрая вероятность, а второй член
\(р(ш|Х,Y)\) – апостериорная вероятность весов модели с учетом данных.

Мы можем думать об этом как о ансамбле моделей, взвешенных по вероятности каждой модели. Действительно, это эквивалентно ансамблю из бесконечного числа нейронных сетей с одинаковой архитектурой, но с разным весом.

Да вот беда! Оказывается, этот интеграл в большинстве случаев неразрешим. Это связано с тем, что апостериорную вероятность нельзя оценить аналитически.

Эта проблема не уникальна для байесовских нейронных сетей. Вы столкнетесь с этой проблемой во многих случаях байесовского обучения, и за эти годы было разработано множество методов для ее преодоления. Мы можем разделить эти методы на два семейства: методы вариационного вывода и методы выборки.

Выборка методом Монте-Карло

У нас есть проблемы. Заднее распределение неразрешимо. Что, если вместо вычисления интеграла по истинному распределению мы аппроксимируем его средним значением выборок, взятых из него? Один из способов сделать это – Цепь Маркова Монте-Карло
— вы строите цепь Маркова с желаемым распределением в качестве равновесного распределения.

Вариационный вывод

Другое решение состоит в том, чтобы аппроксимировать истинное трудноразрешимое распределение другим распределением из поддающегося семейству. Чтобы измерить сходство двух распределений, мы можем использовать расхождение KL:

\(D_ {KL} (p || q) = {\ displaystyle \ int} _ {- \ infty} ^ {\ infty} p (x) log \ frac {p (x)} {q (x)} dx \)

Позволять \(д\) быть вариационным распределением, параметризованным \(\тета\). Мы хотим найти значение \(\тета\) который минимизирует дивергенцию KL:

\begin{split} \theta^* &= \text{argmin}_\theta D_{KL}(q_\theta(w)||p(w|X,Y)) \\ & = \text{argmin} _ \ тета {\ displaystyle \ int} q_ \ theta (w) log \ frac {q_ \ theta (w) p (X, Y)} {p (X, Y | w) p (w)} dw \\ & = \ text {argmin} _ \ theta {\ displaystyle \ int} q_ \ theta (w) log \ frac {q_ \ theta (w)} {p (w)} dw – {\ displaystyle \ int} q_ \ theta ( w) log (p(X,Y|w))dw \\ & = \text{argmin}_\theta D_{KL}(q_\theta(w)||p(w)) – \mathbb{E} _{q_\theta(w)} log(p(X,Y|w)) \end{split}

Посмотрите, что у нас получилось: первый член — это KL-расхождение между вариационным распределением и априорным распределением. Второй член – это вероятность в отношении \(q_\тета\). Итак, мы ищем \(q_\тета\) это лучше всего объясняет данные, но, с другой стороны, максимально близко к априорному распределению. Это просто еще один способ ввести регуляризацию в нейронные сети!

Теперь, когда у нас есть \(q_\тета\) мы можем использовать его, чтобы делать прогнозы:

\(q_\theta(y|x) = {\displaystyle \int} p(y|x,w)q_\theta(w)dw\)

Приведенная выше формулировка исходит из работа DeepMind в 2015 году. Подобные идеи были представлены
могилы в 2011 году и вернуться к Хинтон и ван Кэмп в 1993 году. основной доклад на семинаре NIPS по байесовскому глубокому обучению был очень хороший обзор того, как эти идеи развивались на протяжении многих лет.

Хорошо, но что, если мы не хотим обучать модель с нуля? Что, если у нас есть обученная модель, из которой мы хотим получить оценку неопределенности? Можем ли мы это сделать?

Получается, что если мы используем отсев во время обучения, мы действительно можем.

Профессиональные специалисты по обработке данных размышляют о неопределенности своей модели — иллюстрация

Отсев как средство для неопределенности

Выбывать это хорошо используемая практика в качестве регуляризатора. Во время обучения вы случайным образом выбираете узлы и отбрасываете их, то есть устанавливаете их вывод равным 0. Мотивация? Вы не хотите чрезмерно полагаться на определенные узлы, что может означать переоснащение.

В 2016 году Гал и Гахрамани показал, что если вы также применяете отсев во время вывода, вы можете легко получить оценку неопределенности:

1. сделать вывод \(у|х\) несколько раз, каждый раз выбирая другой набор узлов для исключения.
2. Усредните прогнозы, чтобы получить окончательный прогноз \(\mathbb{Е}(у|х)\).
3. Вычислите выборочную дисперсию прогнозов.

Вот и все! Вы получили оценку дисперсии!
интуиция
За этим подходом стоит то, что тренировочный процесс можно рассматривать как тренировку
\(2^м\) разные модели одновременно — где m — количество узлов в сети: каждое невыпадающее подмножество узлов определяет новую модель. Все модели разделяют веса узлов, которые они не отбрасывают. В каждой партии обучается случайно выбранный набор этих моделей.

После обучения у вас в руках ансамбль моделей. Если вы используете этот ансамбль во время вывода, как описано выше, вы получаете неопределенность ансамбля.

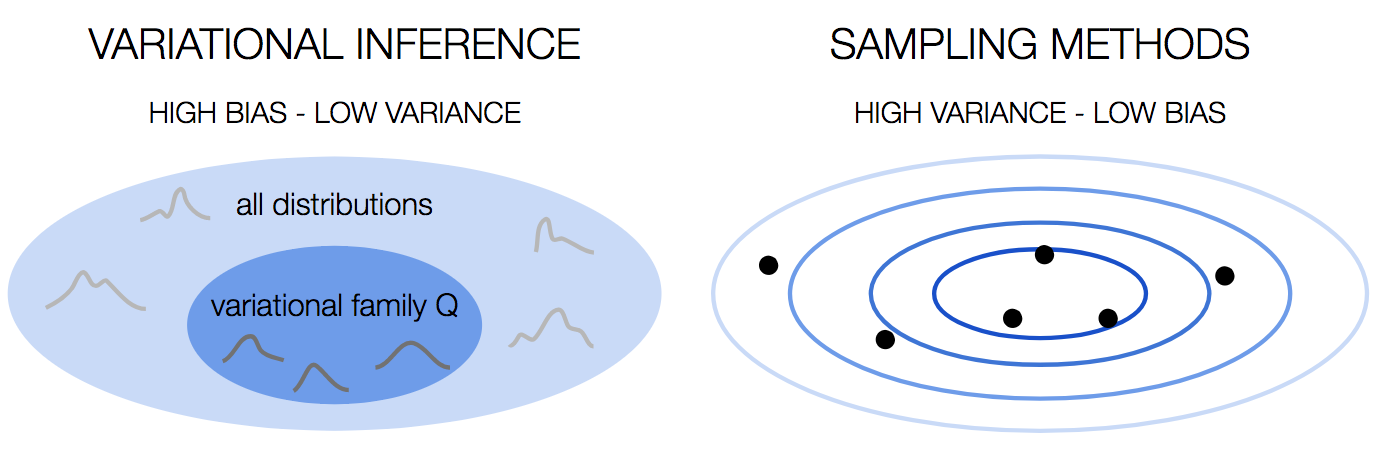
С точки зрения компромисс между смещением и дисперсией, вариационный вывод имеет большое смещение, потому что мы выбираем семейство распределений. Это сильное предположение, которое мы делаем, и, как и любое сильное предположение, оно вносит предвзятость. Однако он стабилен, с низкой дисперсией.

С другой стороны, методы выборки имеют малое смещение, потому что мы не делаем предположений о распределении. Это происходит за счет высокой дисперсии, поскольку результат зависит от образцов, которые мы рисуем.

Возможность оценить неопределенность модели является горячей темой. Важно помнить об этом в приложениях с высоким риском, таких как медицинские помощники и беспилотные автомобили. Это также ценный инструмент для понимания того, какие данные могут принести пользу модели, чтобы мы могли пойти и получить их.

В этом посте мы рассмотрели некоторые подходы к получению оценок неопределенности модели. Есть много других методов, поэтому, если вы чувствуете себя очень неуверенно, ищите больше данных 🙂

В следующем посте мы покажем вам, как использовать неопределенность в рекомендательных системах и, в частности, как справиться с задача разведки-эксплуатации. Следите за обновлениями.

Это второй пост из серии статей, которые мы представляем на семинаре конференции KDD в этом году: сети с высокой плотностью и неопределенность в рекомендательных системах.

Первый пост можно найти
здесь.