В текстовой классификации выбор признаков — это процесс выбора определенного подмножества терминов обучающего набора и использования только их в алгоритме классификации. Процесс выбора признаков происходит до обучения классификатора.

Обновление: платформа машинного обучения Datumbox теперь имеет открытый исходный код и бесплатна для скачать. Ознакомьтесь с пакетом com.datumbox.framework.machinelearning.featureselection, чтобы увидеть реализацию методов хи-квадрата и взаимной информации в Java.

Основные преимущества использования алгоритмов выбора признаков заключаются в том, что они уменьшают размер наших данных, ускоряют обучение и могут повысить точность за счет удаления зашумленных признаков. Как следствие, выбор функций может помочь нам избежать переобучения.

Базовый алгоритм отбора k лучших признаков представлен ниже (Мэннинг и др., 2008 г.):

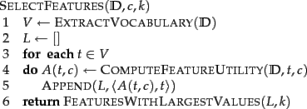
В следующих разделах мы представляем два разных алгоритма выбора признаков: взаимную информацию и хи-квадрат.

Взаимная информация

Одним из наиболее распространенных методов выбора признаков является взаимная информация термина t в классе c (Мэннинг и др., 2008 г.). Это измеряет, сколько информации присутствие или отсутствие определенного термина способствует принятию правильного решения о классификации c. Взаимную информацию можно рассчитать по следующей формуле:

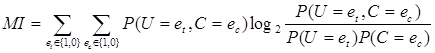(1)

В наших расчетах, поскольку мы используем оценки максимального правдоподобия вероятностей, мы можем использовать следующее уравнение:

(2)

Где N – общее количество документов, N_ткколичество документов, которые имеют значения e_т (наличие термина t в документе; принимает значение 1 или 0) и e_с(вхождение документа в класс c; принимает значение 1 или 0), что указывается двумя нижними индексами, и . Наконец, мы должны отметить, что все вышеупомянутые переменные принимают неотрицательные значения.

Площадь Чи

Другим распространенным методом выбора признаков является Площадь Чи. х² тест используется в статистике, среди прочего, для проверки независимости двух событий. В частности, при выборе признаков мы используем его, чтобы проверить, независимы ли появление определенного термина и появление определенного класса. Таким образом, мы оцениваем следующую величину для каждого термина и ранжируем их по количеству баллов:

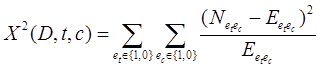(3)

Высокие баллы по х² указывают, что нулевая гипотеза (H₀) независимости следует отклонить и, таким образом, возникновение термина и класса являются зависимыми. Если они зависимы, то мы выбираем признак для классификации текста.

Приведенную выше формулу можно переписать следующим образом:

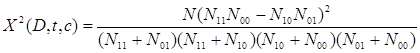(4)

Если мы используем метод хи-квадрат, мы должны выбрать только предопределенное количество объектов, которые имеют ax² результат теста выше 10,83, что указывает на статистическую значимость на уровне 0,001.

И последнее, но не менее важное: мы должны отметить, что со статистической точки зрения выбор функции хи-квадрат неточен из-за одной степени свободы и поправка Йейтса вместо этого следует использовать (что затруднит достижение статистической значимости). Таким образом, следует ожидать, что из общего числа выбранных признаков небольшая часть не зависит от класса). Таким образом, следует ожидать, что из общего числа выбранных признаков небольшая часть не зависит от класса. Тем не менее, как Мэннинг и др. (2008) показали, что эти зашумленные признаки не оказывают серьезного влияния на общую точность нашего классификатора.

Удаление шумных/редких функций

Другой метод, который может помочь нам избежать переобучения, уменьшить потребление памяти и повысить скорость, — удалить из словаря все редкие термины. Например, можно удалить все термины, которые встречались только один раз во всех категориях. Удаление этих терминов может значительно сократить использование памяти и повысить скорость анализа. Наконец, нам не следует, что этот метод можно использовать в сочетании с описанными выше алгоритмами выбора признаков.

Вам понравилась статья? Пожалуйста, найдите минутку, чтобы поделиться им в Твиттере. 🙂