В кооперативном многоагентном обучении с подкреплением (MARL) из-за его политика Обычно считается, что методы градиента политик (PG) менее эффективны в отношении выборки, чем методы декомпозиции значений (VD), которые вне политики. Однако некоторые недавний эмпирический исследования продемонстрировать, что при правильном представлении входных данных и настройке гиперпараметров многоагентный PG может достичь удивительно высокой производительности по сравнению с методами VD вне политики.
Почему методы PG могут работать так хорошо? В этом посте мы представим конкретный анализ, чтобы показать, что в определенных сценариях, например, в средах с очень мультимодальным ландшафтом вознаграждения, VD может быть проблематичным и привести к нежелательным результатам. Напротив, в этих случаях методы PG с отдельными политиками могут сходиться к оптимальной политике. Кроме того, методы PG с авторегрессивными (AR) политиками могут изучать мультимодальные политики.
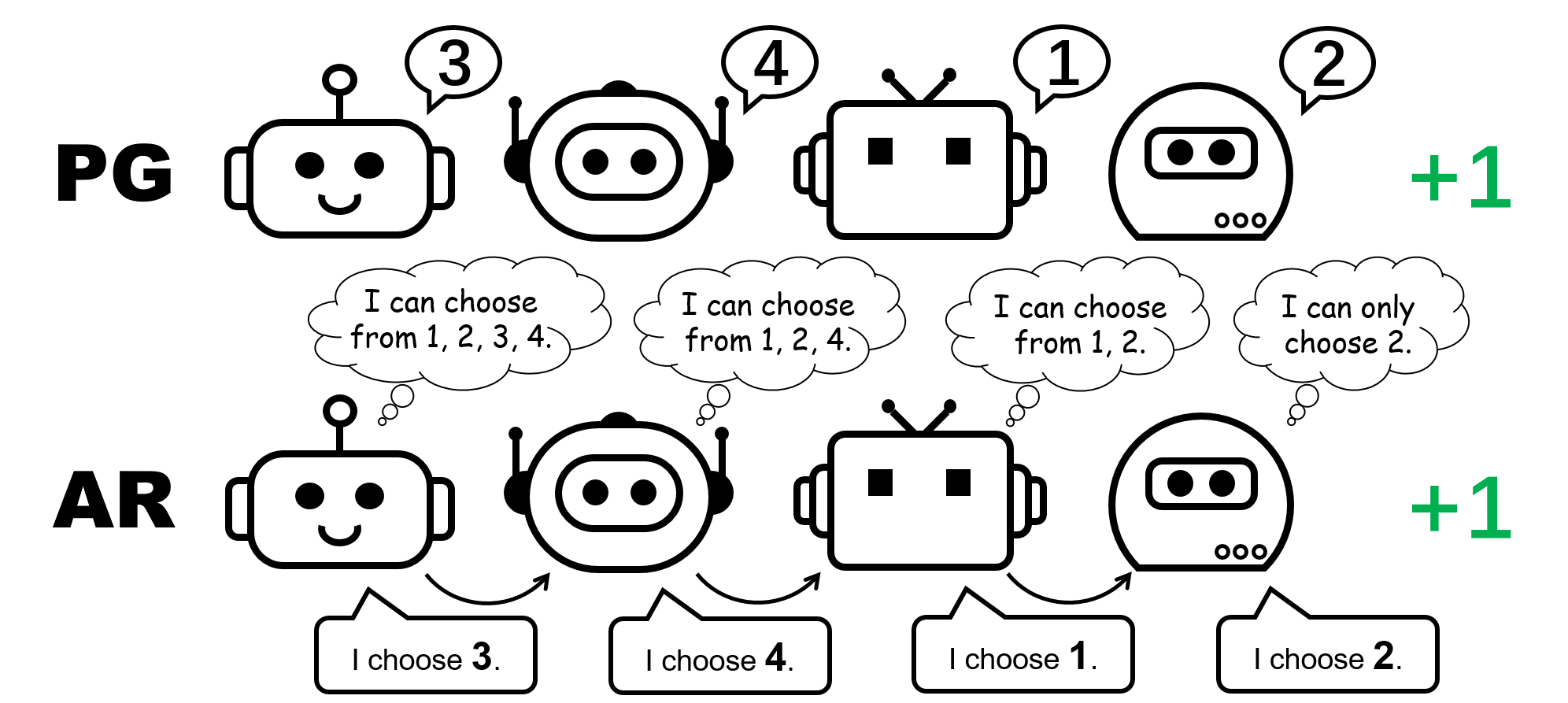
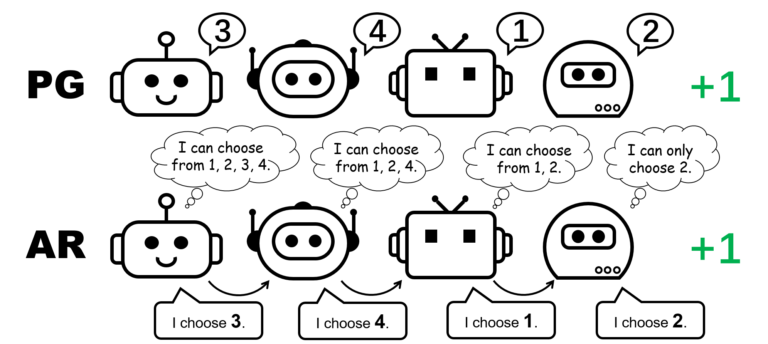
Рисунок 1: другое представление политики для игры с перестановкой для 4 игроков.
CTDE в кооперативном MARL: методы VD и PG
Централизованное обучение и децентрализованное исполнение (CTDE) — популярный фреймворк в кооперативном MARL. Он использует Глобальный информацию для более эффективного обучения при сохранении представления отдельных политик для тестирования. CTDE может быть реализован с помощью декомпозиции значений (VD) или градиента политик (PG), что приводит к двум различным типам алгоритмов.
Методы VD изучают локальные сети Q и функцию смешивания, которая смешивает локальные сети Q с глобальной функцией Q. Функция микширования обычно применяется для удовлетворения индивидуального-глобального-макс.ИГМ), гарантирующий оптимальное совместное действие, можно вычислить путем жадного выбора оптимального действия локально для каждого агента.
Напротив, методы PG напрямую применяют градиент политики для изучения индивидуальной политики и функции централизованного значения для каждого агента. Функция значения принимает в качестве входных данных глобальное состояние (например, МАППО) или объединение всех локальных наблюдений (например, МАДДПГ), для точной глобальной оценки стоимости.
Игра в перестановки: простой контрпример, когда VD терпит неудачу
Мы начнем наш анализ с рассмотрения кооперативной игры без состояния, а именно игры перестановок. В перестановочной игре с участием $N$ каждый агент может произвести $N$ действий ${ 1,\ldots, N }$. Агенты получают вознаграждение $+1$, если их действия взаимно различны, т. е. совместное действие представляет собой перестановку над $1, \ldots, N$; в противном случае они получают вознаграждение в размере 0 долларов США. Заметим, что в этой игре существует $N!$ симметричных оптимальных стратегий.
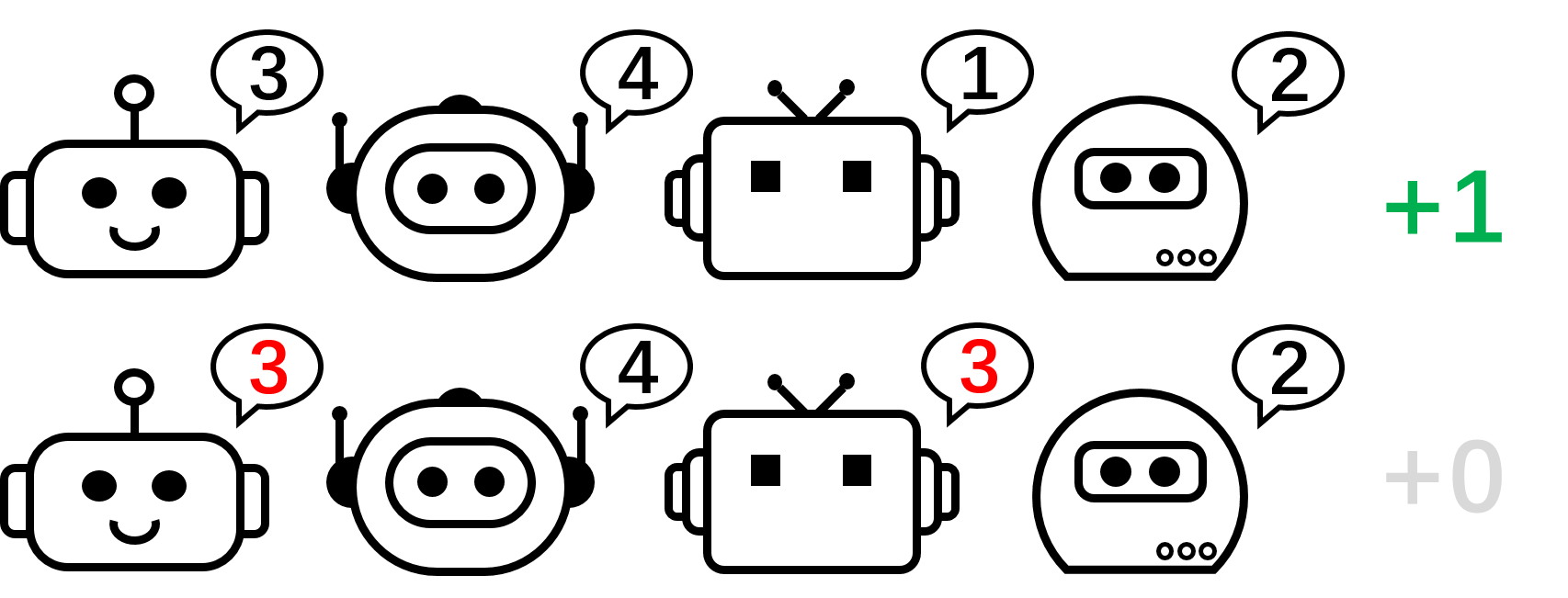
Рисунок 2: игра перестановок для 4 игроков.
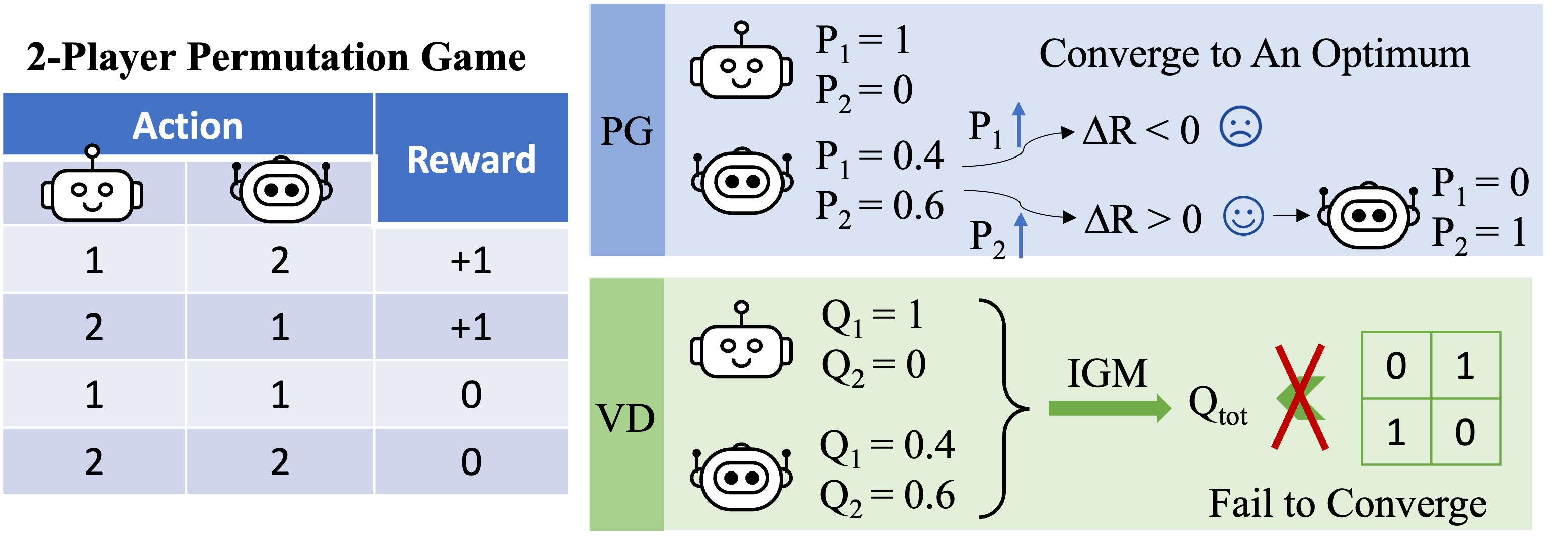
Рисунок 3: Интуитивное представление высокого уровня о том, почему VD терпит неудачу в игре перестановок для двух игроков.
Теперь давайте сосредоточимся на игре с перестановками для двух игроков и применим к ней VD. В этой настройке без сохранения состояния мы используем $Q_1$ и $Q_2$ для обозначения локальных Q-функций и используем $Q_\textrm{tot}$ для обозначения глобальной Q-функции. Принцип IGM требует, чтобы
\(\arg\max_{a^1,a^2}Q_\textrm{tot}(a^1,a^2)=\{\arg\max_{a^1}Q_1(a^1),\ аргумент\макс_{а^2}Q_2(а^2)\}.\)
Мы доказываем, что VD не может представлять выигрыш в игре перестановок двух игроков от противного. Если бы методы VD могли представить выигрыш, мы бы имели
\(Q_\textrm{tot}(1, 2)=Q_\textrm{tot}(2,1)=1\quad \text{and}\quad Q_\textrm{tot}(1, 1)=Q_\ textrm{общий}(2,2)=0.\)
Если любой из этих двух агентов имеет разные локальные значения Q (например, $Q_1(1)> Q_1(2)$), мы имеем $\arg\max_{a^1}Q_1(a^1)=1$. Тогда по принципу ИГМ любой оптимальное совместное действие
\((a^{1\star},a^{2\star})=\arg\max_{a^1,a^2}Q_\textrm{tot}(a^1,a^2)=\ {\ arg \ max_ {a ^ 1} Q_1 (a ^ 1), \ arg \ max_ {a ^ 2} Q_2 (a ^ 2) \} \)
удовлетворяет $a^{1\star}=1$ и $a^{1\star}\neq 2$, поэтому совместное действие $(a^1,a^2)=(2,1)$ является суб- оптимальна, т. е. $Q_\textrm{tot}(2,1)<1$.
В противном случае, если $Q_1(1)=Q_1(2)$ и $Q_2(1)=Q_2(2)$, то
\(Q_\textrm{tot}(1, 1)=Q_\textrm{tot}(2,2)=Q_\textrm{tot}(1, 2)=Q_\textrm{tot}(2,1). \)
В результате декомпозиция значений не может представлять матрицу выигрышей игры с перестановками для двух игроков.
А как насчет методов ПГ? Индивидуальные политики действительно могут представлять оптимальную политику для игры перестановок. Более того, стохастический градиентный спуск может гарантировать сходимость PG к одному из этих оптимумов. при мягких предположениях. Это говорит о том, что, хотя методы PG менее популярны в MARL по сравнению с методами VD, они могут быть предпочтительнее в некоторых случаях, которые распространены в реальных приложениях, например, в играх с несколькими модальностями стратегии.
Мы также отмечаем, что в игре перестановок, чтобы представить оптимальную совместную политику, каждый агент должен выбирать различные действия. Следовательно, успешная реализация PG должна гарантировать, что политики зависят от агента. Это можно сделать с помощью либо отдельных политик с неразделяемыми параметрами (называемых в нашей статье PG-Ind), либо политики, обусловленной идентификатором агента (PG-ID).
PG превосходит существующие методы VD на популярных испытательных стендах MARL
Выходя за рамки простого иллюстративного примера игры с перестановками, мы расширяем наше исследование на популярные и более реалистичные тесты MARL. В дополнение к мультиагентному испытанию StarCraft (СМАК), где была проверена эффективность входных данных политик PG и обусловленных агентами, мы показываем новые результаты в Google Research Football (ГРФ) и мультиплеер Ханаби вызов.
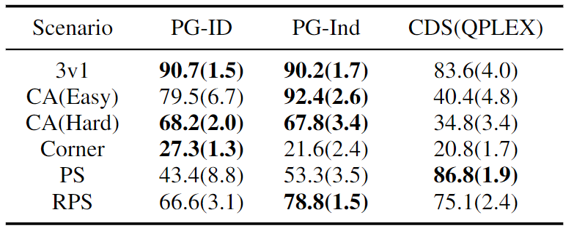
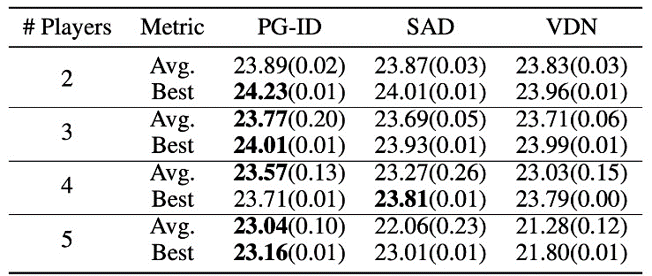
Рисунок 4: (слева) коэффициенты выигрыша методов PG на GRF; (справа) лучшие и средние оценки на Hanabi-Full.
В GRF методы PG превосходят современные базовые методы VD (CDS) в 5 случаях. Интересно, что мы также заметили, что отдельные политики (PG-Ind) без совместного использования параметров обеспечивают сопоставимые, а иногда и более высокие показатели выигрыша по сравнению с политиками для конкретных агентов (PG-ID) во всех 5 сценариях. Мы оцениваем PG-ID в полномасштабной игре Hanabi с разным количеством игроков (2-5 игроков) и сравниваем их с ГРУСТНЫЙсильный вариант Q-обучения вне политики в Hanabi и сети декомпозиции ценности (ВДН). Как показано в приведенной выше таблице, PG-ID может давать результаты, сравнимые или даже лучше, чем лучшие и средние вознаграждения, достигнутые SAD и VDN, с различным количеством игроков, использующих одинаковое количество шагов среды.
Помимо более высоких вознаграждений: изучение мультимодального поведения с помощью авторегрессивного моделирования политики
Помимо обучения более высоким вознаграждениям, мы также изучаем, как изучать мультимодальные политики в кооперативном MARL. Вернемся к игре перестановок. Хотя мы доказали, что PG может эффективно обучаться оптимальной политике, режим стратегии, которого он в конечном итоге достигает, может сильно зависеть от инициализации политики. Таким образом, закономерным будет вопрос:
Можем ли мы выучить единую политику, которая может охватывать все оптимальные режимы?
В децентрализованной формулировке PG факторизованное представление совместной политики может представлять только один конкретный режим. Поэтому мы предлагаем расширенный способ параметризации политик для большей выразительности — авторегрессивные (AR) политики.

Рисунок 5: сравнение индивидуальных политик (PG) и авторегрессивных политик (AR) в игре перестановок с 4 игроками.
Формально разложим совместную политику $n$ агентов в виде
\(\pi(\mathbf{a} \mid \mathbf{o}) \ приблизительно \prod_{i=1}^n \pi_{\theta^{i}} \left(a^{i}\mid o ^{i},a^{1},\ldots,a^{i-1} \right),\)
где действие, производимое агентом $i$, зависит от его собственного наблюдения $o_i$ и всех действий предыдущих агентов $1,\dots,i-1$. Авторегрессионная факторизация может представлять любой совместная политика в централизованной MDP. только модификация политики каждого агента — это входное измерение, которое немного расширяется за счет включения предыдущих действий; и выходное измерение политики каждого агента остается неизменным.
При таких минимальных затратах на параметризацию политика AR существенно улучшает представление методов PG. Отметим, что PG с политикой AR (PG-AR) может одновременно представлять все оптимальные режимы политики в игре перестановок.

Рисунок: тепловые карты действий для политик, изученных PG-Ind (слева) и PG-AR (в центре), и тепловая карта для вознаграждений (справа); в то время как PG-Ind сходится только к определенному режиму в игре перестановок с 4 игроками, PG-AR успешно обнаруживает все оптимальные режимы.
В более сложных средах, включая SMAC и GRF, PG-AR может изучать интересные эмерджентные модели поведения, требующие сильной координации внутри агента, которые PG-Ind может никогда не изучить.
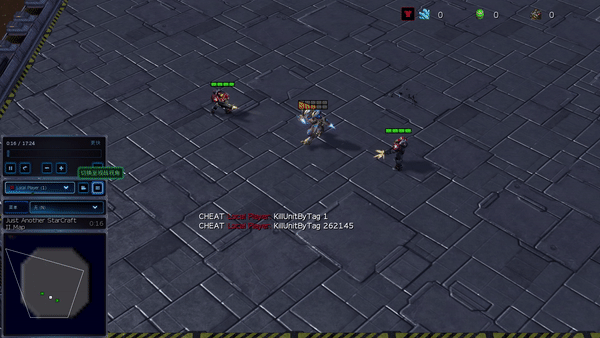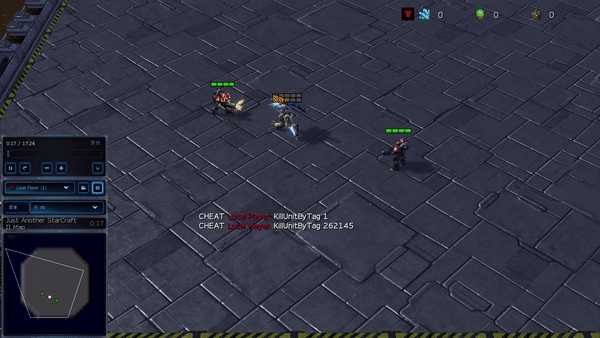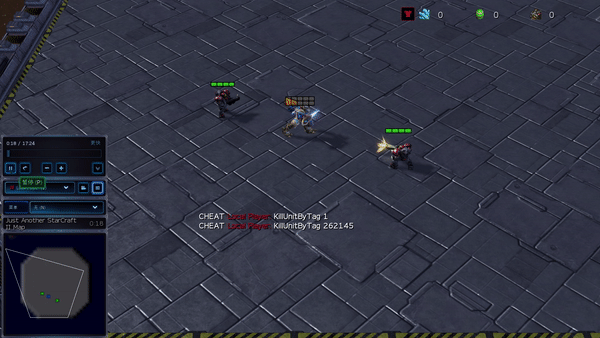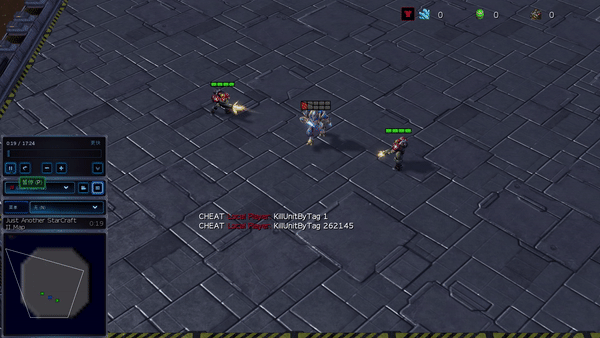
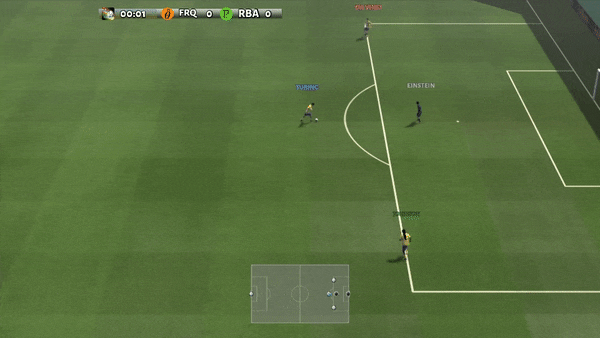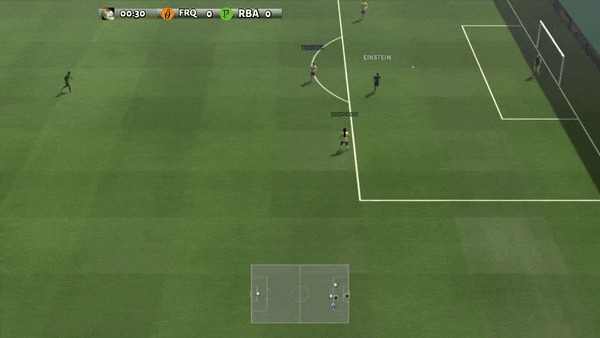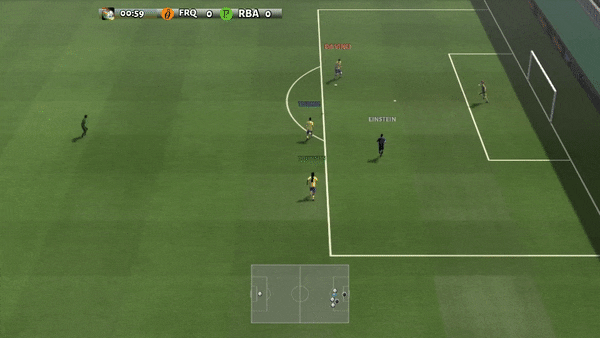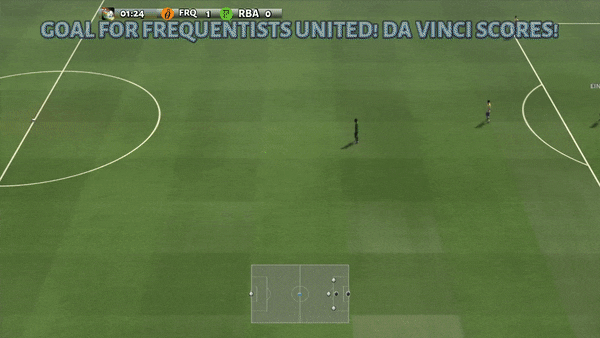
Рисунок 6: (слева) возникающее поведение, вызванное PG-AR в SMAC и GRF. На карте SMAC 2m_vs_1z морские пехотинцы продолжают стоять и атаковать поочередно, при этом гарантируется, что на каждом временном шаге есть только один атакующий морской пехотинец; (справа) в сценарии academy_3_vs_1_with_keeper в GRF агенты учатся поведению в стиле «тики-така»: каждый игрок продолжает передавать мяч своим товарищам по команде.
Обсуждения и выводы
В этом посте мы предоставляем конкретный анализ методов VD и PG в кооперативном MARL. Во-первых, мы раскрываем ограничение выразительности популярных методов VD, показывая, что они не могут представлять оптимальные политики даже в простой игре перестановок. Напротив, мы показываем, что методы PG доказуемо более выразительны. Мы эмпирически проверяем преимущество PG в выразительности на популярных тестовых стендах MARL, включая SMAC, GRF и Hanabi Challenge. Мы надеемся, что выводы из этой работы могут помочь сообществу в создании более общих и мощных алгоритмов кооперативного MARL в будущем.
Этот пост основан на нашей статье: Пересмотр некоторых распространенных практик в совместном многоагентном обучении с подкреплением (бумага, Веб-сайт).