Итак, Deepmind выпустил новый бумага несколько дней назад под названием «Нейронно-арифметико-логические единицы» (НАЛУ). После победа AlphaGo против лучшего игрока в го в мире, каждая новая статья DeepMind вызывает волнение в сообществе ИИ. Но на этот раз весь этот пух того стоит. Хорошо, тогда что такое NALU и какова его цель?
Зачем нам нужны НАЛУ?
Нейронные сети доказали свою сверхъестественную способность изучать сложные функции из любых данных, будь то числа, изображения или звук. Но у них есть существенный недостаток: они не умеют считать. Я имею в виду, что они не могут выводить значения за пределами диапазона обучающих данных.
Например, если у нас есть тренировочный набор с диапазоном от 0 до 100, выходные данные также будут находиться в этом же диапазоне. Неважно, какую функцию активации или какой метод оптимизации мы используем, результат всегда будет внутри этого диапазона. Итак, если мы хотим построить счетчик с нейросетью, мы не можем передавать ему следующие данные
(0,1,2,3,4,5) и ожидаем вывести 6. Ниже приведен интересный график, который показывает именно это:

(нейронные арифметико-логические блоки)(https://arxiv.org/pdf/1808.00508.pdf) : MLP изучают функцию идентификации только для значений диапазона, на которых они обучены. Средняя ошибка резко возрастает как ниже, так и выше диапазона чисел, наблюдаемых во время обучения. Кредит: Траск и др.
Что такое НАЛУ?
Вы можете возразить, что это несколько существенное ограничение глубокого обучения, и я с вами согласен. Вот где NALU приходит на место. NALU использует тщательную комбинацию вентилей и расширяет модель нейронного аккумулятора (NAC). NAC на самом деле представляет собой линейное преобразование и может накапливать входные данные аддитивно.

(нейронные арифметико-логические блоки)(https://arxiv.org/pdf/1808.00508.pdf)
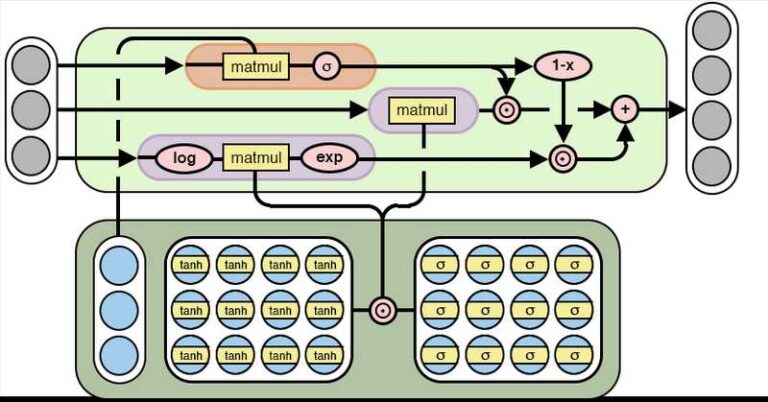
NALU расширяет функциональные возможности сложения и вычитания NAC и может представлять умножение и деление. Он состоит из двух ячеек NAC (одна для сложения и одна для умножения), интерполированных обученным сигмоидальным вентилем.

(нейронные арифметико-логические блоки)(https://arxiv.org/pdf/1808.00508.pdf)

(нейронные арифметико-логические блоки)(https://arxiv.org/pdf/1808.00508.pdf)
Ясно, что не очень легко объяснить, почему ворота имеют именно такую структуру, потому что это результат сложных математических принципов и инструментов. Слава исследователям. Однако важно то, что теперь эти блоки можно использовать в любой известной модели, от сверточных сетей до автоэнкодеров, и расширить их возможности. Примеры практических приложений, которые уже исследованы авторами и дают многообещающие результаты:
- Изучите простые арифметические функции
- Подсчитайте, сколько рукописных символов появляется на изображении
- Преобразование текстовых выражений в числовые значения
- Отслеживание времени в среде Grid-World
Для получения дополнительной информации о вышеизложенном, пожалуйста, прочитайте статью. И вы должны, потому что мы говорим о некоторых интересных вещах.
Реализация на Python
Давайте теперь попробуем построить NALU с помощью Tensorflow и Python и сами проверим, насколько хорошо они работают. У нас есть уравнения, у нас есть красивое графическое представление. Это не должно быть так сложно. Верно? И это действительно не так.
Если мы будем следовать математическим выражениям, появившимся выше, мы получим:
import tensorflow as tf
def NALU(prev_layer, num_outputs):
eps=1e-7
shape = (int(prev_layer.shape(-1)),num_outputs)
W_hat = tf.Variable(tf.truncated_normal(shape, stddev=0.02))
M_hat = tf.Variable(tf.truncated_normal(shape, stddev=0.02))
W = tf.tanh(W_hat) * tf.sigmoid(M_hat)
a = tf.matmul(prev_layer, W)
G = tf.Variable(tf.truncated_normal(shape, stddev=0.02))
m = tf.exp(tf.matmul(tf.log(tf.abs(prev_layer) + eps), W))
g = tf.sigmoid(tf.matmul(prev_layer, G))
out = g * a + (1 - g) * m
return out
Ну вот и все! Теперь давайте построим простую нейронную сеть исключительно с помощью NALU и используем ее для изучения простой математической функции. Сначала давайте создадим некоторые фиктивные данные для обучения и тестирования нашей модели:
arithmetic_functions={
'add': lambda x,y :x+y,
}
def get_data(N, op):
split = 4
X_train = np.random.rand(N, 10)*10
a = X_train(:, :split).sum(1)
b = X_train(:, split:).sum(1)
Y_train = op(a, b)(:, None)
print(X_train.shape)
print(Y_train.shape)
X_test = np.random.rand(N, 10)*100
a = X_test(:, :split).sum(1)
b = X_test(:, split:).sum(1)
Y_test = op(a, b)(:, None)
print(X_test.shape)
print(Y_test.shape)
return (X_train,Y_train),(X_test,Y_test)
Обратите внимание, что тестовый набор имеет гораздо больший диапазон, чем набор поездов. Цель этой разницы – проверить, насколько хорошо модель может экстраполировать. Теперь нам нужно создать сеанс тензорного потока и запустить алгоритм обратного распространения.
tf.reset_default_graph()
train_examples=10000
(X_train,Y_train),(X_test,Y_test)=get_data(train_examples,arithmetic_functions('add'))
X = tf.placeholder(tf.float32, shape=(train_examples, 10))
Y = tf.placeholder(tf.float32, shape=(train_examples, 1))
X_1=NALU(X,2)
Y_pred=NALU(X_1,1)
loss = tf.nn.l2_loss(Y_pred - Y)
optimizer = tf.train.AdamOptimizer(0.1)
train_op = optimizer.minimize(loss)
with tf.Session() as session:
session.run(tf.global_variables_initializer())
for ep in range(50000):
_,pred,l = session.run((train_op, Y_pred, loss),
feed_dict={X: X_train, Y: Y_train})
if ep % 1000 == 0:
print('epoch {0}, loss: {1}'.format(ep,l))
_,test_predictions,test_loss = session.run((train_op, Y_pred,loss),feed_dict={X:X_test,Y:Y_test})
print(test_loss)
Потеря (среднеквадратическая ошибка) на тестовом наборе оказалась равной 8,575397e-05. Удивительный! Его практически ноль. Обратите внимание, что тестовые данные имели другой диапазон обучающих данных, поэтому мы можем сделать вывод, что экстраполяция F (x, y) = x + y почти идеальна. Конечно, мы можем проверить это на других простых функциях. Результаты будут такими же хорошими.
Понятно, что применение нейронных арифметико-логических блоков (NALU) практически безгранично, поскольку их можно использовать буквально в каждой существующей модели для повышения ее производительности и расширения их возможностей за пределы диапазона обучающих данных.
* Раскрытие информации: Обратите внимание, что некоторые из приведенных выше ссылок могут быть партнерскими ссылками, и без дополнительной оплаты для вас мы будем получать комиссию, если вы решите совершить покупку после перехода по ссылке.