В исследовательском проекте ISO для получения степени магистра машинного обучения в Имперском колледже Лондона я сосредоточился на проблеме кластерного анализа с использованием смешанных моделей процесса Дирихле. DPMM — это «полностью байесовский» метод обучения без учителя, который, в отличие от других методов кластерного анализа, не требует от нас предварительного определения общего количества кластеров в наших данных. Крупные компании, такие как Google, используют эти бесконечные смешанные модели Дирихле в различных приложениях, включая классификацию документов, обработку естественного языка, компьютерное зрение и другие.

Обновление: платформа машинного обучения Datumbox теперь имеет открытый исходный код и бесплатна для скачать. Ознакомьтесь с пакетом com.datumbox.framework.machinelearning.clustering, чтобы увидеть реализацию смешанных моделей процессов Дирихле в Java.

Во время моего исследования у меня была возможность работать с двумя разными смешанными моделями: многомерной нормальной смешанной моделью, которая используется для кластеризации непрерывных гауссовых наборов данных, и полиномиальной смешанной моделью Дирихле, которая используется для кластеризации документов. Первоначальное исследование длилось 3 месяца и проводилось под руководством профессора Альдо Фейсал из Имперского колледжа Лондона. Я планирую в течение следующих недель опубликовать адаптированную версию моего исследования в этом блоге, обсудить теорию и приложения смешанных моделей процессов Дирихле и опубликовать реализацию Java, которую можно использовать для выполнения кластеризации с помощью DPMM.

Эта статья является введением/обзором исследования, описывает проблемы, кратко обсуждает модели смешения процесса Дирихле и, наконец, представляет структуру предстоящих статей.

1. Обзор методов кластерного анализа

Кластерный анализ — это метод обучения без учителя, целью которого является выявление групп в наборе данных. Группы выбираются таким образом, чтобы отнесенные к ним наблюдения были более похожи друг на друга, чем на наблюдения, принадлежащие разным группам. Кластеризация — это неконтролируемый метод, поскольку он не использует аннотированные наборы данных для оценки вышеупомянутых кластеров. Вместо этого кластеры идентифицируются только с использованием характеристик/особенностей данных.

Задача кластерного анализа не связана напрямую с конкретным алгоритмом, а существует несколько различных подходов к моделированию данных. В литературе мы можем найти центроидные модели (такие как K-средние и K-представитель), которые представляют группы как средние векторы, модели распределения (например, смесь гауссианов), которые моделируют генеративные распределения данных с использованием статистики и вероятностей, Кластеризация графа модели (такие как MCL), которые организуют наборы данных на основе краевой структуры наблюдений, модели связности (такие как Агломеративный и Разделительный алгоритмы), которые ориентированы на дистанционную связь и многое другое.

Алгоритмы кластерного анализа могут быть дополнительно разделены на разные категории в зависимости от того, как они организуют кластеры. Например, алгоритмы можно разделить в зависимости от того, выполняют ли они жесткую или мягкую кластеризацию (назначение точек данных одному кластеру или множеству кластеров с определенной вероятностью/весом), а также в зависимости от того, выполняют ли они плоскую, иерархическую или перекрывающуюся кластеризацию (сохраняют ли иерархию). в выявленных кластерах).

Наконец, учитывая тот факт, что кластерный анализ является одним из самых популярных и регулярно используемых методов машинного обучения, в литературе было предложено несколько различных алгоритмов и моделей. В общем, метод, который используется в каждом случае, сильно зависит от проблемы и типа данных, которые у нас есть.

2. Применение кластеризации

Благодаря тому, что кластерный анализ не требует наличия аннотированных наборов данных, которые обычно дороги и их трудно найти, он стал мощным инструментом во многих различных областях науки и бизнеса. В результате кластеризация имеет множество приложений в большом количестве различных областей.

В компьютерном зрении кластеризация часто используется при сегментации изображений и группировании различных объектов в сцене. В биоинформатике и нейробиологии его можно использовать для группировки генов или нейронов, связанных с конкретными задачами/поведением. В маркетинге и бизнес-кластеризации он регулярно используется для определения групп в клиентских базах данных и позволяет компаниям предлагать более целенаправленные услуги. Поисковые системы используют кластеризацию, чтобы идентифицировать похожие документы в своих индексах и организовывать веб-страницы по категориям. Социальные сети используют кластеризацию для идентификации сообществ и клик внутри больших групп пользователей. Наконец, следует отметить, что кластерный анализ успешно применяется в ряде других областей, таких как медицина, информатика, финансы, социальные науки, робототехника, физика и других.

3. Задача определения количества Кластеров

Одной из самых сложных проблем кластеризации является определение общего количества кластеров, существующих в данных. В общем, многие из существующих алгоритмов требуют общее количество кластеров k в качестве параметра перед выполнением анализа, и их результаты сильно зависят от этого параметра. Когда количество кластеров k заранее известно, вышеупомянутые алгоритмы могут предоставить нам требуемые кластерные назначения. Тем не менее, это число редко известно в реальных приложениях. Кроме того, во многих приложениях ожидается изменение количества кластеров по мере добавления новых наблюдений с течением времени.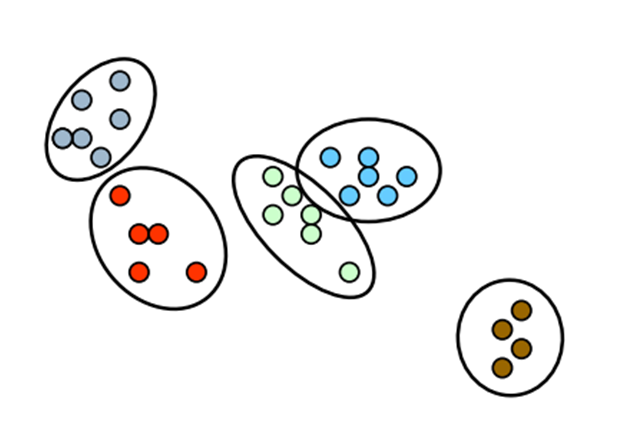

Несмотря на то, что было предложено несколько методов, позволяющих избежать прямого указания количества кластеров (Агломеративная иерархическая кластеризация) или оценить оптимальное количество кластеров по данным (таким как Х-означает), большинство методов передают эвристику и не используют вероятностную структуру. Один альтернативный подход, который позволяет нам динамически оценивать количество кластеров и адаптировать его по мере наблюдения большего количества данных, заключается в использовании смешанных моделей процессов Дирихле.

4. Обзор моделей смеси процесса Дирихле

Процесс Дирихле — это семейство непараметрических байесовских моделей, которые обычно используются для оценки плотности. полупараметрическое моделирование и выбор модели/усреднение. Процессы Дирихле непараметричны в том смысле, что они имеют бесконечное число параметров. Поскольку они рассматриваются в байесовском подходе, мы можем строить большие модели с бесконечными параметрами, которые мы интегрируем, чтобы избежать переобучения. Можно показать, что ДП могут быть представлены различными способами, каждый из которых математически эквивалентен. Несколько распространенных способов представить процесс Дирихле – это схема урны Блэквелла-Маккуина, конструкция ломания палки и процесс китайского ресторана.

Модели смеси процессов Дирихле могут быть построены для выполнения кластеризации в наборах данных. С помощью DPMM мы строим единую модель смеси, в которой количество компонентов смеси бесконечно. Это означает, что DPMM не требует, чтобы мы с самого начала определяли количество кластеров (которое в данном случае бесконечно), и позволяет нам адаптировать количество активных кластеров по мере того, как мы вводим больше данных в нашу модель с течением времени.

Как мы увидим в следующей статье, представление DPMM как процесса китайского ресторана создает эффект кластеризации, который мы используем для выполнения кластерного анализа данных. Чтобы оценить кластерные назначения нашей модели, мы можем использовать выборку Гиббса и, следовательно, мы должны выбрать соответствующие сопряженные априорные значения, чтобы сделать выборку возможной.

5. Применение DPMM

Модели смеси процессов Дирихле стали популярными как в машинном обучении, так и в статистике. Следовательно, они использовались в большом количестве приложений. Вуд и др. использовали DPMM для сортировки спайков и определения количества различных нейронов, которые контролировались одним электродом. Саддерт и др. использовали эту модель для выполнения анализа визуальной сцены и определения количества объектов, частей и особенностей, содержащихся в конкретном изображении. Лян и др. и Финкель и др. использовали иерархические процессы Дирихле в области обработки естественного языка, чтобы определить, сколько грамматических символов существует в определенном наборе предложений. Окончательно Блей и др. и Тех и др. использовали аналогичные иерархические модели для кластеризации документов на основе их семантических категорий.

6. Мотивация

DPMM становятся все более популярными и активно исследуются. Они были применены к большому количеству различных проблем и решают многие из вышеупомянутых ограничений кластерного анализа в рамках вероятностной структуры. DPMM позволяют нам выполнять обучение без учителя, используя непараметрический и полностью байесовский подход, и строить сложные модели с иерархической структурой.

Поэтому в этой серии статей я сосредоточусь на представлении математических основ модели, обсуждении различных представлений процессов Дирекле, представлю две разные модели: многомерную нормальную смешанную модель и полиномиальную смешанную модель Дирихле, которые можно использовать для кластеризации непрерывных данных. и документы, и, наконец, я представлю свою реализацию Java и результаты демонстраций.

7. Предстоящие посты/структура

Эта серия статей будет иметь ту же структуру, что и мой исследовательский отчет, и будет разделена на следующие сегменты:

1. Обзор кластерного анализа и моделей смеси процесса Дирихле: Обзор различных методов кластерного анализа и их приложений, описание проблемы оценки количества кластеров и обзор DPMM и их приложений.
2. Модель конечной смеси, основанная на распределении Дирихле: Обсуждаются основы бета-распределений и распределений Дирихле, вводятся априорная модель Дирихле с полиномиальной моделью правдоподобия и модель конечных смесей с распределением Дирихле.
3. Процесс Дирихле, китайский ресторанный процесс и другие представления: Дает определение процесса Дирихле, представляет различные представления DP и фокусируется на процессе китайского ресторана.
4. Модель смеси процесса Дирихле: Представляет модель смеси процесса Дирихле, предоставляет альтернативную модель, в которой используется процесс китайского ресторана, и описывает пробоотборник Collapsed-Gibbs, который используется для оценки кластерных назначений.
5. Кластеризация документов и гауссовских данных с помощью моделей смеси процесса Дирихле: Обсуждается, как выполнить кластеризацию с помощью DPMM, и представлена ​​многомерная нормальная смешанная модель Дирихле и полиномиальная смешанная модель Дирихле.
6. Кластеризация с помощью модели смеси процессов Дирихле в Java: Предоставляет обзор моей Java-реализации многомерной нормальной смешанной модели и полиномиальной смешанной модели Дирихле, а также демонстрацию.

Следите за следующими статьями! Надеюсь, вам понравился этот пост; если вы это сделали, пожалуйста, найдите время, чтобы поделиться статьей на Facebook и Twitter. 🙂