Этот пост в блоге является четвертой частью серии статей о кластеризации с использованием моделей смеси процессов Дирихле. В предыдущих статьях мы обсуждали модели конечных смесей Дирихле и взяли предел их модели для бесконечных k кластеров, что привело нас к введению процессов Дирихле. Как мы видели, наша цель — построить смешанную модель, которая не требует от нас указывать количество k кластеров/компонентов с самого начала. После представления различных представлений процессов Дирихле пришло время фактически использовать DP для построения бесконечной смешанной модели, которая позволяет нам выполнять кластеризацию. Целью этой статьи является определение смешанных моделей процесса Дирихле и обсуждение использования китайского ресторанного процесса и отбора проб Гиббса. Если вы не читали предыдущие посты, настоятельно рекомендуем это сделать, так как тема немного теоретическая и требует хорошего понимания конструкции модели.

Обновление: платформа машинного обучения Datumbox теперь имеет открытый исходный код и бесплатна для скачать. Ознакомьтесь с пакетом com.datumbox.framework.machinelearning.clustering, чтобы увидеть реализацию смешанных моделей процессов Дирихле в Java.

1. Определение модели смеси процесса Дирихле

Использование процессов Дирихле позволяет нам иметь смешанную модель с бесконечными компонентами, которую можно рассматривать как ограничение конечной модели для k до бесконечности. Предположим, что у нас есть следующая модель:

Уравнение 1: Модель смеси процесса Дирихле

Где G определяется как и используется как краткое обозначение которая представляет собой дельта-функцию, которая принимает 1, если и 0 в другом месте. θ_я – параметры кластера, выбранные из G. Генеративное распределение F настраивается параметрами кластера θ_я и используется для генерации x_я наблюдения. Наконец, мы можем определить распределение плотности что является нашим распределением смеси (счетная бесконечная смесь) с пропорциями смешивания и смешивание компонентов .

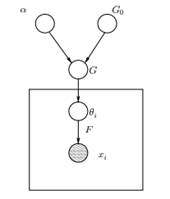
Рисунок 1: Графическая модель модели смеси процесса Дирихле

Выше мы можем видеть эквивалентную графическую модель DPMM. Г₀ является базовым распределением DP, и обычно оно выбирается сопряженным перед нашим порождающим распределением F, чтобы упростить вычисления и использовать привлекательные математические свойства. α — это скалярный гиперпараметр процесса Дирихле, который влияет на количество кластеров, которые мы получим. Чем больше значение α, тем больше кластеров; чем меньше α, тем меньше кластеров. Следует отметить, что значение α выражает сила веры в G₀. Большое значение указывает на то, что большинство выборок будут различны и будут иметь значения, сосредоточенные на G.₀. G – это случайное распределение в пространстве параметров Θ, выбранное из DP, которое назначает вероятности параметрам. θ_я – вектор параметров, который берется из распределения G и содержит параметры кластера, распределение F параметризуется θ_я и х_я является точкой данных, сгенерированной генеративным распределением F.

Важно отметить, что θ_я являются элементами пространства параметров Θ и «конфигурируют» наши кластеры. Их также можно рассматривать как скрытые переменные на x_я которые говорят нам, из какого компонента/кластера x_я откуда и каковы параметры этого компонента. Таким образом, для каждого х_я что мы наблюдаем, мы рисуем θ_я из распределения G. С каждым розыгрышем распределение меняется в зависимости от предыдущих выборов. Как мы видели на схеме урны Блэквелла-МакКуина, распределение G можно интегрировать, и наш будущий выбор θ_я зависят только от G₀: . Оценка параметров θi по предыдущей формуле не всегда осуществима, поскольку многие реализации (например, процесс китайского ресторана) включают перечисление через экспоненциально возрастающие компоненты k. Таким образом, используются приблизительные вычислительные методы, такие как выборка Гиббса. Наконец, мы должны отметить, что хотя k кластеров бесконечно, количество активных кластеров равно . Таким образом,_я будет повторяться и проявлять эффект кластеризации.

2. Использование процесса китайского ресторана для определения модели бесконечной смеси

Модель, определенная в предыдущем сегменте, является математически надежной, однако у нее есть существенный недостаток: для каждого нового x_я что мы наблюдаем, мы должны выбрать новый θ_я с учетом предыдущих значений θ. Проблема в том, что во многих случаях выборка этих параметров может быть сложной и дорогостоящей задачей.

Альтернативный подход заключается в использовании процесса китайского ресторана для моделирования скрытых переменных z._я кластерных заданий. Таким образом, вместо использования θ_я для обозначения как параметров кластера, так и назначений кластера мы используем скрытую переменную z_я чтобы указать идентификатор кластера, а затем использовать это значение для назначения параметров кластера. В результате нам больше не нужно выбирать θ каждый раз, когда мы получаем новое наблюдение, вместо этого мы получаем назначение кластера путем выборки z._я из ЦРП. В этой схеме новое θ выбирается только тогда, когда нам нужно создать новый кластер. Ниже мы представляем модель этого подхода:

Уравнение 2: Модель смеси с CRP

Выше приведена генеративная модель, описывающая, как данные x_я и создаются кластеры. Для проведения кластерного анализа мы должны использовать наблюдения x_я и оценим кластерные назначения z_я.

3. Вывод модели смеси и выборка Гиббса

К сожалению, поскольку процессы Дирихле непараметричны, мы не могу использовать алгоритм EM для оценки скрытых переменных, в которых хранятся назначения кластера. Для оценки заданий воспользуемся Свернутая выборка Гиббса.

Свернутая выборка Гиббса — это простой алгоритм Монте-Карло с цепями Маркова (MCMC). Это быстро и позволяет нам интегрировать некоторые переменные при выборке другой переменной. Тем не менее этот алгоритм требует от нас выбора G₀ который является сопряженным априором генеративного распределения F, чтобы иметь возможность аналитически решать уравнения и иметь возможность выбирать непосредственно из .

Шаги свернутой выборки Гиббса, которые мы будем использовать для оценки кластерных назначений, следующие:

• Инициализировать z_я кластерные назначения случайным образом
• Повторять до схождения
• Выбрать случайно топор_я
  
• Держите другой г_Дж фиксировано для каждого j≠i:
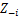
• Присвойте новое значение z_я путем расчета «вероятности CRP», которая зависит от z_Дж и х_Дж всех j≠i:

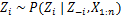
В следующей статье мы сосредоточимся на том, как выполнять кластерный анализ с использованием моделей Dirichlet Process Mixture. Мы определим две разные смешанные модели процесса Дирихле, которые используют процесс китайского ресторана и свернутую выборку Гиббса для выполнения кластеризации непрерывных наборов данных и документов.