Что такое совместное распределение в машинном обучении?

Нейронные сети

Что такое совместное распределение в машинном обучении? | DeepTech

DEEPTECH

September 22, 2023

Введение

Совместное распределение, также известное как совместное распределение вероятностей, рассчитывает вероятность того, что два события произойдут вместе и в один и тот же момент времени. Совместная вероятность — это вероятность того, что два события могут произойти одновременно. Вероятность — это раздел математики, изучающий возникновение случайных событий. Проще говоря, это вероятность определенного события. Эта концепция часто используется в статистическом анализе, но ее также можно использовать в машинном обучении в качестве стратегии классификации для создания генеративных моделей.

Читайте также: Что такое Argmax в машинном обучении?

Что такое совместное распределение, момент и изменение?

Вероятность очень важна в области науки о данных. Оно выражается числом от 0 до 1 включительно, где 0 указывает на невероятную вероятность возникновения события, а 1 обозначает определенный исход события. Например, вероятность вытянуть красную карту из колоды карт равна 1/2 = 0,5. Это означает, что существует равная вероятность вытянуть красное и черное; поскольку в колоде 52 карты, из которых 26 красных и 26 черных, вероятность вытянуть красную карту против черной карты составляет 50-50.

При создании алгоритмов ученым, работающим с данными, часто приходится делать выводы, основанные на статистике. Затем это будет использоваться для лучшего прогнозирования или анализа данных. Статистический вывод относится к процессу, который используется для поиска свойств, существующих в распределении вероятностей. Одно из таких распределений известно как совместное распределение или совместная вероятность.

Совместную вероятность можно определить как вероятность того, что два или более событий произойдут одновременно. Эти два события обычно обозначаются событием A и событием B. В терминологии вероятности это можно записать как р(А и Б). Следовательно, совместная вероятность — это вероятность того, что два события могут произойти одновременно.

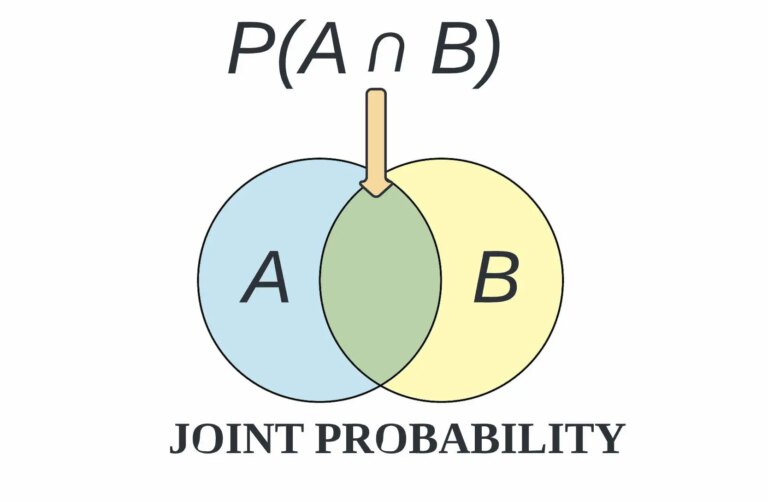
Совместную вероятность также можно описать как вероятность пересечения или несоответствия областей двух или более событий. В статистике это записывается как p(A ∩ B). Сопоставление совместного распределения по субъектам используется в машинном обучении, чтобы помочь определить взаимосвязь, которая может существовать, а может и не существовать между двумя случайными величинами. Совместное распределение вероятностей можно применять только в ситуациях, когда одновременно может происходить более одного наблюдения.

Например, из колоды из 52 карт совместная вероятность вытащить карту, одновременно красную и 6, равна P(6 ∩ красная) = 2/52 = 1/26, поскольку в колоде карт есть две красные шестерки — шестерка червей и шестерка бубен.

Время от времени в литературе по машинному обучению появляются термины «первый момент» и «второй момент». Так что же означает момент в контексте машинного обучения? Короче говоря, первый момент набора чисел — это просто среднее или среднее значение, а второй момент — это обычно просто дисперсия. Дисперсия — это среднеквадратическая разница между каждой точкой данных и центром распределения, измеренным средним значением.

Предположим, у вас есть четыре числа (x0, x1, x2, x3). Первый необработанный момент равен (x0^1 + x1^1 + x2^1 + x3^1)/4, что является не чем иным, как средним значением. Например, если ваши четыре числа (2, 3, 6, 9), то первый необработанный момент будет

(2^1 + 3^1 + 6^1 + 9^1) / 4 = (2 + 3 + 6 + 9) / 4 = 20/4 = 5,0

Другими словами, чтобы вычислить необработанный первый момент набора чисел, вы возводите каждое число до 1, суммируете, а затем делите на количество чисел. Второй необработанный момент набора чисел аналогичен первому моменту, за исключением того, что вместо того, чтобы повышать каждое число до 1, вы увеличиваете его до 2, что также известно как возведение числа в квадрат.

Другими словами, второй необработанный момент четырех чисел равен (x0^2 + x1^2 + x2^2 + x3^2)/4. Для (2, 3, 6, 9) второй необработанный момент равен

(2^2 + 3^2 + 6^2 + 9^2) / 4 = (4 + 9 + 36 + 81) / 4 = 130/4 = 32,5.

Помимо первого и второго необработанных моментов, есть еще центральный момент, когда перед возведением в степень вы вычитаете среднее значение.

Например, второй центральный момент четырех чисел равен ((x0-m)^2 + (x1-m)^2 + (x2-m)^2 + (x3-m)^2)/4. Для (2 , 3, 6, 9), второй центральный момент равен

((2-5)^2 + (3-5)^2 + (6-5)^2 + (9-5)^2) / 4 = (9 + 4 + 1 + 16) / 4 = 30/ 4 = 7,5

Это дисперсия совокупности четырех чисел. Мы не рассчитываем первый центральный момент, потому что он всегда будет равен нулю. Общая цель моментов в машинном обучении также состоит в том, чтобы сообщить нам определенные свойства распределения, такие как среднее значение, характеристики временной области, эффективные функции и степень искажения распределения.

Вариация или дисперсия также важны в машинном обучении, поскольку они могут проявляться в результатах классификации и помогают выявить несоответствия совместного распределения. Обсуждая точность модели и эффективность классификации, нам необходимо помнить об ошибках прогнозирования, которые включают в себя смещение и дисперсию, которые всегда будут связаны с любой эффективной моделью машинного обучения. Всегда будет небольшая разница в наших целевых и исходных образцах. Эти различия называются ошибками.

Цель аналитика – не устранить ошибки, а уменьшить их. Смещение — это разница между нашими фактическими и прогнозируемыми значениями. Смещение — это простые предположения, которые наша модель делает в отношении наших данных, чтобы иметь возможность прогнозировать новые данные. Когда смещение велико, предположения, сделанные в нашей модели, слишком просты, и модель не может отразить важные особенности наших данных. Это означает, что наша модель не уловила закономерности в обучающих данных и, следовательно, не может хорошо работать и на тестовых данных. В этом случае наша модель не сможет работать с новыми данными и не может быть отправлена в производство. Этот случай, когда модель не может найти закономерности в нашем обучающем наборе и, следовательно, не работает как для видимых, так и для невидимых данных, называется недостаточным подбором.

Дисперсия является полной противоположностью предвзятости. Во время обучения это позволяет нашей модели просматривать данные определенное количество раз, чтобы находить в них закономерности. Если он не работает с данными достаточно долго, он не сможет обнаружить закономерности и возникнет систематическая ошибка. С другой стороны, если нашей модели разрешено просматривать данные слишком много раз, она будет очень хорошо обучаться только этим данным. Он улавливает большинство закономерностей в данных, но также обучается на имеющихся ненужных данных или на шуме. Мы можем определить дисперсию как чувствительность модели к колебаниям данных.

Наша модель может учиться на шуме. Это заставит нашу модель считать тривиальные функции важными. Высокая дисперсия в серии обучающих выборок приводит к переобучению модели машинного обучения. Для любой модели мы должны найти идеальный баланс между смещением и дисперсией. Это просто гарантирует, что мы уловим основные закономерности в нашей модели, игнорируя при этом присутствующий в них шум. Это называется компромиссом смещения-дисперсии. Это помогает оптимизировать ошибку в нашей модели и свести ее к минимуму. Оптимизированная модель будет чувствительна к закономерностям в наших данных, но в то же время сможет обобщать ее на новые данные.

Источник: YouTube

Условия совместной вероятности

Помните, что совместная вероятность — это вероятность пересечения двух или более событий, записанная как p(A ∩ B). Есть два условия совместной вероятности, как показано ниже:

Во-первых, события X и Y должны произойти одновременно. Например, одновременное бросание двух игральных костей.

Во-вторых, события X и Y должны быть независимы друг от друга. Это означает, что

исход события X не влияет на результат события Y. Например, бросание двух игральных костей.

Если выполнены следующие условия, то P(A∩B) = P(A) * P(B).

Совместную вероятность нельзя использовать для определения того, насколько возникновение одного события влияет на возникновение другого события. Следовательно, совместная вероятность X и Y (двух зависимых событий) будет равна P(Y). Совместная вероятность двух непересекающихся событий будет равна 0, поскольку оба события не могут произойти вместе. Чтобы события считались зависимыми, необходимо иметь влияние на то, насколько вероятно другое. Другими словами, зависимое событие может произойти только в том случае, если другое событие произойдет раньше. Например, предположим, что вы хотите поехать в отпуск в конце следующего месяца, но это зависит от наличия достаточного количества денег для оплаты поездки.

Возможно, вы рассчитываете на бонус, комиссию или аванс к своей зарплате. Это также, скорее всего, зависит от того, будет ли вам предоставлен отпуск в последнюю неделю месяца для поездки. Для зависимых событий вместо совместной вероятности используется условная вероятность. Событие считается независимым, если оно не связано с другим событием или вероятностью его наступления или, наоборот, с ненаступлением. Например, цвет ваших волос совершенно не влияет на то, где вы работаете. Независимые события не влияют друг на друга и не влияют на вероятность другого события. Совместная вероятность также может использоваться для задач многомерной классификации.

Применение в машинном обучении

Совместная вероятность — это одна из многих формул вероятности, которые находят применение в машинном обучении. Это связано с тем, что вероятностные предположения делаются на основе неопределенных данных. Это чрезвычайно распространено в алгоритмах распознавания образов и других подходах к классификации. Распознавание образов — это процесс распознавания образов с использованием алгоритма машинного обучения, который включает в себя классификацию изображений. Распознавание образов можно определить как классификацию данных на основе уже полученных знаний или статистической информации, извлеченной из шаблонов и/или их представления.

Одним из важных аспектов распознавания образов является его прикладной потенциал. В типичном приложении для распознавания образов необработанные данные обрабатываются и преобразуются в форму, пригодную для использования машиной. Распознавание образов включает в себя классификацию и кластеризацию образов. При классификации соответствующая метка класса присваивается шаблону на основе абстракции, созданной с использованием набора обучающих шаблонов или знаний предметной области. Классификация используется в контролируемом обучении.

Существует множество различных типов алгоритмов классификации, таких как классификация сигналов MI-ЭЭГ, классификация ЭЭГ на основе LSTM, классификация сигналов ЭЭГ между субъектами и классификация образов движений. Кластеризация генерирует раздел данных, который помогает принимать решения, конкретную интересующую нас деятельность по принятию решений. Кластеризация используется в обучении без учителя. Шаблоны состоят из отдельных признаков, которые могут быть непрерывными, дискретными или даже дискретными двоичными переменными, или наборов признаков, оцениваемых вместе, известных как вектор признаков.

Самым большим преимуществом является то, что эта модель генерирует классификацию с некоторым уровнем достоверности для каждой точки данных и часто выявляет тонкие, скрытые закономерности, которые нелегко увидеть человеческой интуицией. Как правило, чем больше переменных признаков запрограммирован на проверку алгоритма и чем больше точек данных доступно для обучения, тем точнее он будет.

Это применимо независимо от того, помечен или не помечен целевой домен или исходный домен. Совместное распространение также создает основу для трансферного обучения и глубокого трансфера для адаптации через компонент трансфера. Трансферное обучение — это метод машинного обучения, при котором модель, разработанная для задачи, повторно используется в качестве отправной точки для модели для второй задачи. Это популярный подход в глубоком обучении, при котором предварительно обученные модели используются в качестве отправной точки для задач компьютерного зрения и обработки естественного языка, учитывая огромные вычислительные и временные ресурсы, необходимые для разработки моделей нейронных сетей для решения этих задач, а также огромный скачок в навыках. которые они предоставляют по смежным проблемам.

Читайте также: Переоснащение и недостаточное оснащение в алгоритмах машинного обучения

Заключение

В заключение, совместное распространение является важной частью машинного обучения. В основном это связано с тем, насколько важны алгоритмы распознавания образов в современном мире. Они используются в распознавании речи, идентификации говорящего, распознавании мультимедийных документов (MDR), автоматической медицинской диагностике и сетях для извлечения признаков. Это также помогает сделать ИИ умнее и быстрее. Существуют также другие типы распределений вероятностей, используемые в машинном обучении, такие как условные распределения и маргинальные распределения. Дополнительную информацию по этой теме можно найти на Stack Exchange, который представляет собой доску вопросов и ответов для вопросов по науке о данных. Спасибо, что прочитали эту статью.