Я обучался по специализации Эндрю Нг по глубокому обучению на Coursera. Прошел 1-й из 5-ти курсов по специализации (Нейронные сети и глубокое обучение).

Я нахожусь на втором, который улучшает глубокое обучение. Это очень интересный курс, который углубляется в настройку гиперпараметров, методы регуляризации и оптимизации.

1. Что такое алгоритмы оптимизации?

Они позволяют вам обучать вашу нейронную сеть намного быстрее, поскольку прикладное машинное обучение — это эмпирический процесс, эти алгоритмы помогают эффективно достигать оптимизированных результатов.

Давайте начнем изучать алгоритмы оптимизации с более сложной версии градиентного спуска.

1.1 Пакетный и мини-пакетный градиентный спуск

В общем, Gradient Descent перебирает весь набор обучающих примеров (#m) и делает один шаг к глобальным минимумам. Это также называется пакетным градиентным спуском. Это довольно неэффективно, потому что требует от нас пройти все обучающие примеры, прежде чем сделать крошечный шаг к минимумам.

Как насчет того, чтобы использовать меньший фрагмент/выборку тренировочного набора, чтобы делать пошагово? Это не что иное, как мини-пакетный градиентный спуск. Это означает, что мы делим входной обучающий набор (X) и целевой набор (Y) на небольшие пакеты, называемые мини-пакетами, и проходим каждый пакет, чтобы сразу сделать шаг к минимуму. Это значительно улучшает скорость, с которой сходится градиентный спуск.

Чтобы сделать это еще быстрее, как насчет того, чтобы сделать шаг градиентного спуска для каждого обучающего примера? Давайте посмотрим, какие последствия будут на изображении ниже.

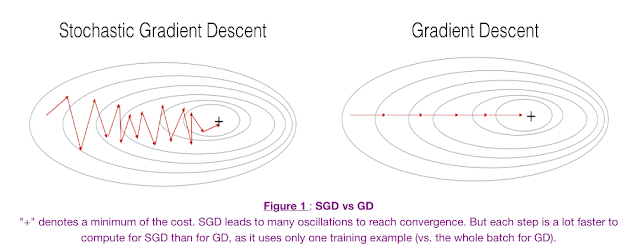
Источник: Специализация глубокого обучения — задание по программированию (оптимизация).

1. Слева у нас стохастический градиентный спуск (где m = 1 на шаг), мы делаем шаг градиентного спуска для каждого примера, а справа — пакетный градиентный спуск (1 шаг на весь тренировочный набор).
2. SGD кажется достаточно шумным, в то же время он намного быстрее, но может не сходиться к минимуму.
3. Как правило, чтобы получить лучшее из обоих миров, мы используем мини-пакетный градиентный спуск (MGD), который одновременно рассматривает меньшее количество примеров тренировочного набора (обычно степень 2 – 2 ^ 6 и т. д.).
4. Мини-пакетный градиентный спуск относительно более стабилен, чем стохастический градиентный спуск (SGD), но имеет колебания, поскольку шаги градиента выполняются в направлении образца обучающего набора, а не всего набора, как в BGD.

1.2 Как уменьшить колебания при использовании мини-пакетного градиентного спуска (MGD)?

Существует множество методов, доступных для уменьшения колебаний, включая использование предыдущих шагов градиента в качестве эталона, чтобы убедиться, что мы идем в правильном направлении минимума. Эти методы обычно включают использование усреднения по окну, чтобы обеспечить более плавные шаги для уменьшения колебаний.

На изображении выше показан результат пакетного градиентного спуска. Как видите, вывод стоимости очень шумный. Когда мы используем такие методы, как экспоненциальное усреднение веса, как у Адама (Adaptive Momentum Estimation), выходная стоимость становится более плавной, как показано ниже.

1.3 Затухание скорости обучения

Это еще один важный метод, используемый для оптимизации алгоритмов обучения. По мере того, как мы приближаемся к глобальному минимуму, мы хотим, чтобы наш алгоритм делал небольшие шаги и не перескакивал или не колебался вокруг минимума. Обычно это делается с помощью различных способов снижения скорости обучения за эпоху.

Самый простой способ уменьшить скорость обучения — установить ее на половину от предыдущей величины каждую эпоху.

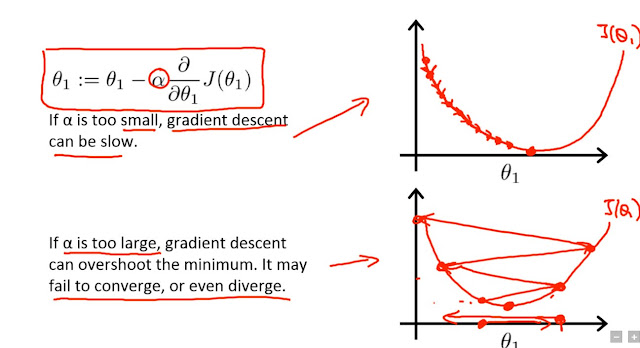Источник: Coursera Эндрю Нг — курс машинного обучения.

Примечание. Эпоха — это один проход через весь обучающий набор.