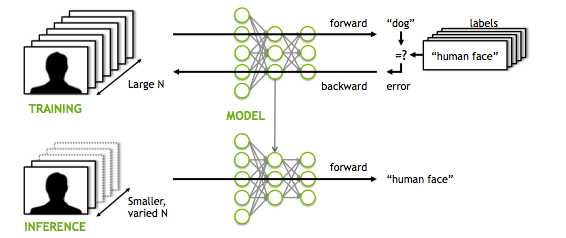
В этой части мы собираемся изучить, как мы можем улучшить нашу библиотеку нейронной сети, добавив структуру сверточной нейронной сети для использования в наборе данных изображений. Никто не может утверждать, что сверточные нейронные сети — лучший способ классификации и обучения изображений, и именно поэтому они так широко используются в системах компьютерного зрения. Цель, конечно же, состоит в том, чтобы снова использовать GPU и OpenCL, поскольку ConvNets требуют больше вычислительных ресурсов и памяти, чем обычные полносвязные сети.
Давай начнем. Прежде всего, мы должны помнить, что CovNets в их более простых формах состоят из сверточного слоя, слоя пула и полносвязного слоя. К счастью, мы реализовали последний. Так что остается только два первых.
Сверточный слой
На этот раз я не буду вдаваться в подробности о части C++ и о том, как мы будем строить базовую структуру нашей ConvNet (я сделал это в первой части для полносвязных слоев), но я углублюсь в код ядра, который я думаю самое интересное. В этих слоях мы сворачиваем входное изображение с ядром небольшого размера и получаем карту страха.
kernel void convolve(global float *image, global Filter* filters, global float * featMap,int filterWidth,int inWidth,int featmapdim){
const int xIn=get_global_id(0);
const int yIn=get_global_id(1);
const int z=get_global_id(2);
float sum=0;
for (int r=0;r<filterWidth;r++){
for (int c=0;c<filterWidth;c++){
sum+= filters(z).weights(c*filterWidth +r)*image((xIn+c)+inWidth*(yIn+r));
}
}
sum +=filters(z).bias;
featMap((xIn+yIn*featmapdim +z*featmapdim*featmapdim)) =relu(sum);
}
Как вы понимаете, мы исходим из гипотезы о том, что каждый пиксель карты объектов вычисляется параллельно, поскольку он по своей сути независим от всех остальных. Итак, если у нас есть образ 28×28 и мы используем ядро 5×5, нам потребуется 24×24=576 потоков для одновременной работы. Обратное распространение немного сложнее, потому что не так много онлайн-ресурсов, которые действительно предоставляют уравнения для сверточного слоя.
Если мы переведем вышеприведенное в код C, мы получим:
kernel void deltas(global Node * nodes,global Node * nextnodes,global float *deltas,global int *indexes,int dim,int nextnumNodes,int pooldim){
const int xIn=get_global_id(0);
const int yIn=get_global_id(1);
const int z=get_global_id(2);
int i = xIn+yIn*pooldim +z*pooldim*pooldim;
float delta = 0;
for (int j = 0; j !=nextnumNodes; j++)
delta += nextnodes(j).delta * nextnodes(j).weights(i);
delta *= devsigmoid(nodes(i).output);
for(int r=0;r<2;r++){
for(int c=0;c<2;c++){
if((c*2+r)==indexes(i))
deltas((2*xIn+r)+(2*yIn+c)*dim+z*dim*dim)=delta;
}
}
}
kernel void backpropcnn( global float* featMap,global float* deltas,global Filter* filters,int featmapdim,int imagedim,int filterdim,float a,global float* Image){
const int xIn=get_global_id(0);
const int yIn=get_global_id(1);
const int z=get_global_id(2);
float sum=0;
for (int r=0;r<featmapdim;r++){
for (int c=0;c<featmapdim;c++){
sum+= deltas((c+r*featmapdim +z*featmapdim*featmapdim))*Image((xIn+r)+imagedim *(yIn+c));
}
}
filters(z).weights((xIn+filterdim *yIn)) -=a*sum;
}
Объединенный слой
Объединение слоев — это просто преобразование карты объектов в новую карту меньшего размера. Существует два вида объединения: среднее и максимальное объединение, причем второе используется чаще всего. В максимальном пуле мы просто определяем фильтр (обычно размером 2×2) и применяем его к карте объектов. Цель фильтра — просто извлечь максимальное значение окна фильтра из изображения.
kernel void pooling( global float* prevfeatMap,global float* poolMap,global int* indexes,int Width,int pooldim){
const int xIn=get_global_id(0);
const int yIn=get_global_id(1);
const int z=get_global_id(2);
float max=0;
int index = 0;
for (int r=0;r<2;r++){
for (int c=0;c<2;c++){
if(prevfeatMap((yIn+c)*Width*z +(xIn+r))>max){
max=prevfeatMap((yIn+c)*Width*z +(xIn+r));
index=c*2+r;
}
}
}
poolMap((xIn+yIn*pooldim +z*pooldim*pooldim))=max;
indexes((xIn+yIn*pooldim +z*pooldim*pooldim))=index;
}
Так же, как обратное распространение что касается, фактических расчетов градиента не производится. Все, что нам нужно сделать, это повысить дискретизацию матрицы. Фактически мы передаем градиент на «победившей единице» прямого распространения. Именно по этой причине мы строим и индексируем матрицу в приведенном выше фрагменте ранее, в которой мы сохраняем положение всех «выигрышных единиц». Эта функциональность видна в функции «дельты», которая отвечает за расчет ошибок градиента.
Чтобы запустить код ядра, мы выполняем следующие шаги:
-
Передайте данные в матричном формате (для этого можно использовать OpenCV)
-
Определите cl: Buffers и cl::Kernels
-
Запустите ядра со следующим кодом:
convKern.setArg(0, d_InputBuffer);convKern.setArg(1, d_FiltersBuffer);convKern.setArg(2, d_FeatMapBuffer);
convKern.setArg(3, filterdim);convKern.setArg(4, inputdim);convKern.setArg(5, featmapdim);
err = (OpenCL::clqueue).enqueueNDRangeKernel(convKern, cl::NullRange,
cl::NDRange(featmapdim, featmapdim, convLayer.numOfFilters),
cl::NullRange);
poolKern.setArg(0, d_FeatMapBuffer);poolKern.setArg(1, d_PoolBuffer);poolKern.setArg(2, d_PoolIndexBuffer);
poolKern.setArg(3, featmapdim);poolKern.setArg(4, pooldim);
err = (OpenCL::clqueue).enqueueNDRangeKernel(poolKern, cl::NullRange,
cl::NDRange(pooldim, pooldim, convLayer.numOfFilters),
cl::NullRange);
deltasKern.setArg(0, d_layersBuffers(0));deltasKern.setArg(1, d_layersBuffers(1));deltasKern.setArg(2, d_deltasBuffer);deltasKern.setArg(3, d_PoolIndexBuffer);
deltasKern.setArg(4, featmapdim);deltasKern.setArg(5, h_netVec(1));deltasKern.setArg(6, pooldim);
err = (OpenCL::clqueue).enqueueNDRangeKernel(deltasKern, cl::NullRange,
cl::NDRange(pooldim, pooldim,convLayer.numOfFilters),
cl::NullRange);
backpropcnnKern.setArg(0, d_FeatMapBuffer);backpropcnnKern.setArg(1, d_rotatedImgBuffer);backpropcnnKern.setArg(2, d_FiltersBuffer);
backpropcnnKern.setArg(3, featmapdim);backpropcnnKern.setArg(4, inputdim);backpropcnnKern.setArg(5, filterdim);
backpropcnnKern.setArg(6, lr);backpropcnnKern.setArg(7, d_InputBuffer);
err = (OpenCL::clqueue).enqueueNDRangeKernel(backpropcnnKern, cl::NullRange,
cl::NDRange(filterdim, filterdim,convLayer.numOfFilters),
cl::NullRange);
Это было не так уж плохо, верно? Если вы должны получить только одну вещь из двух постов, так это то, что нейронные сети и глубокое обучение в целом — это не что иное, как операции между матрицами, которые пытаются аппроксимировать математическую функцию. Даже если эта функция заключается в том, как водить машину. Мы видели, что создать библиотеку нейронной сети с нуля и даже запрограммировать ее для работы на графическом процессоре не так уж и сложно. Все, что вам нужно, это базовое понимание линейной алгебры и представление о том, как работают графические процессоры.
Еще раз напомню, что полный код можно найти в моем репозитории на github. Библиотека нейронных сетей
* Раскрытие информации: Обратите внимание, что некоторые из приведенных выше ссылок могут быть партнерскими ссылками, и без дополнительной оплаты для вас мы будем получать комиссию, если вы решите совершить покупку после перехода по ссылке.