Более века назад, Шриниваса Рамануджан потряс математический мир своей экстраординарной способностью видеть в числах замечательные закономерности, которые не мог видеть никто другой. Математик-самоучка из Индии описал свои прозрения как глубоко интуитивные и духовные, и закономерности часто приходили ему в ярких снах. Эти наблюдения запечатлели потрясающую красоту и чистую возможность абстрактного мира чистой математики. В последние годы мы стали свидетелями прорывов ИИ в области, связанные с глубокой человеческой интуициейа в последнее время и на некоторых самые сложные проблемы в наукаходнако до сих пор новейшие методы искусственного интеллекта не помогли добиться значительных результатов в чисто математических исследованиях.

Как часть Миссия DeepMind Чтобы решить проблему интеллекта, мы исследовали потенциал машинного обучения (МО) для распознавания математических структур и закономерностей и помощи математикам в совершении открытий, которые они иначе никогда бы не открыли, — впервые продемонстрировав, что ИИ может помочь в авангарде чистой математики.

Наша исследовательская работа, опубликованный сегодня в журнале Nature, подробно описывает наше сотрудничество с ведущими математиками с целью применения ИИ для открытия новых идей в двух областях чистой математики: топологии и теории представлений. С Профессор Джорди Уильямсон в Университете Сиднея мы обнаружили новую формулу гипотезы о перестановках, которая оставалась нерешенной десятилетиями. С Профессор Марк Лакенби и Профессор Андраш Юхас в Оксфордском университете мы обнаружили неожиданную связь между разными областями математики, изучая структуру узлов. По словам ведущих математиков, рецензировавших работу, это первые значительные математические открытия, сделанные с помощью машинного обучения. Мы также публикуем полные сопутствующие статьи по arXiv для каждого результата, который будет отправлен в соответствующие математические журналы (бумага перестановок; узлы бумаги). На этих примерах мы предлагаем модель того, как эти инструменты могут использоваться другими математиками для достижения новых результатов.

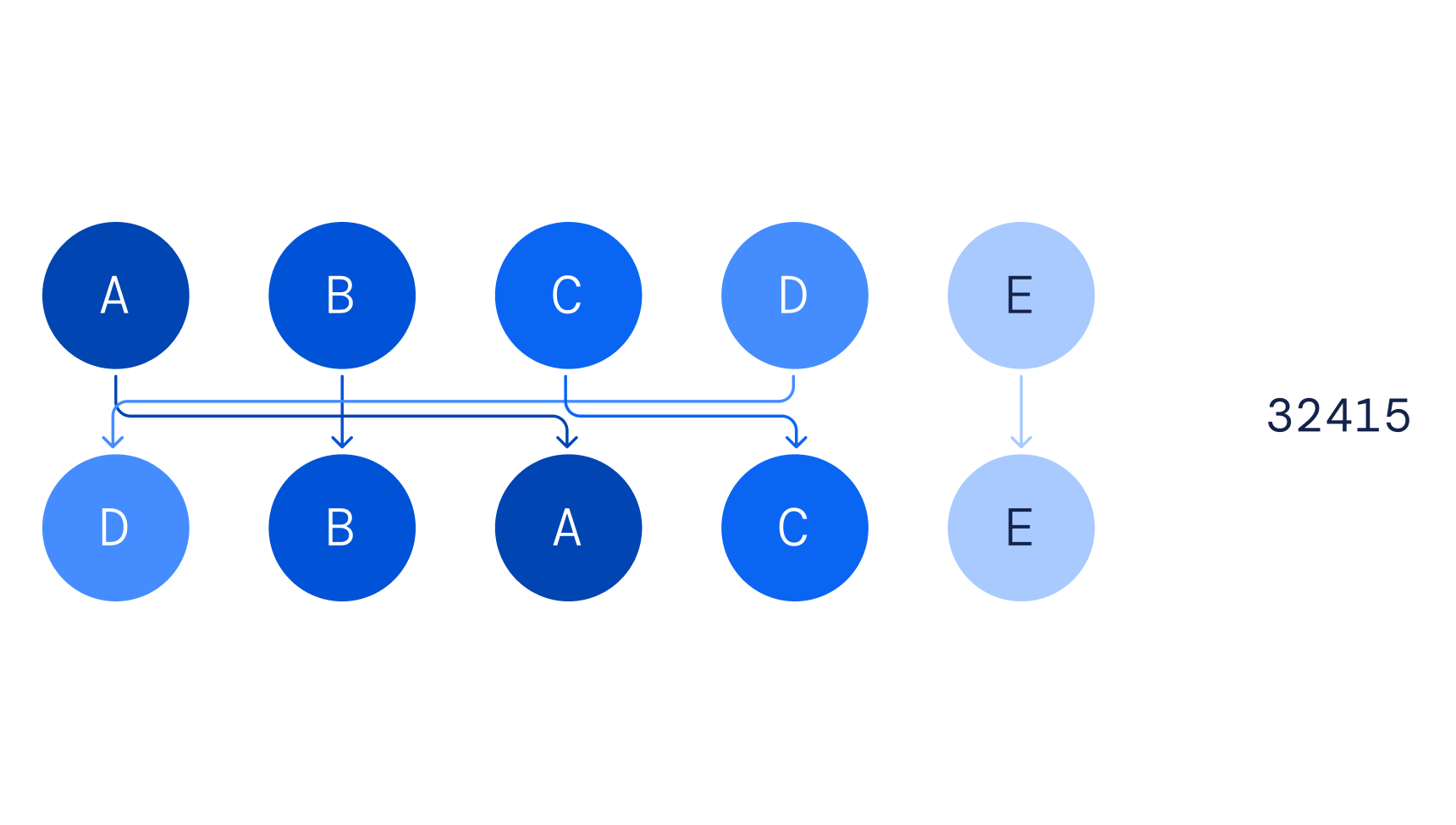
Двумя фундаментальными объектами, которые мы исследовали, были узлы и перестановки.

В течение многих лет компьютеры использовались математиками для генерации данных, помогающих в поиске закономерностей. Этот вид исследований, известный как экспериментальная математика, привел к хорошо известным гипотезам, таким как Гипотеза Берча и Суиннертона-Дайера – один из шести Проблемы премии тысячелетия, самые известные открытые задачи по математике (с призом в 1 миллион долларов США за каждую). Хотя этот подход был успешным и довольно распространенным, идентификация и обнаружение закономерностей из этих данных по-прежнему полагались в основном на математиков.

Нахождение закономерностей стало еще более важным в чистой математике, потому что теперь можно генерировать больше данных, чем любой математик может разумно ожидать изучить за всю жизнь. Некоторые интересующие объекты — например, объекты с тысячами измерений — также могут быть просто непостижимыми, чтобы рассуждать о них напрямую. Помня об этих ограничениях, мы полагали, что ИИ сможет расширить знания математиков совершенно по-новому.

Это похоже на то, как если бы Галилей взял в руки телескоп и смог заглянуть глубоко во вселенную данных и увидеть то, чего раньше не замечал.
Маркус Дю Сотуа , профессор Симони по вопросам общественного понимания науки и профессор математики Оксфордского университета

Наши результаты показывают, что машинное обучение может дополнять математические исследования, чтобы направлять интуицию в отношении проблемы, обнаруживая существование гипотетических паттернов с контролируемым обучением и давая представление об этих паттернах с помощью методов атрибуции машинного обучения:

Вместе с профессором Уильямсоном мы использовали ИИ, чтобы найти новый подход к давней гипотезе в теории представлений. Бросив вызов прогрессу на протяжении почти 40 лет, гипотеза комбинаторной инвариантностиутверждает, что между определенными ориентированными графами и полиномами должна существовать связь. Используя методы машинного обучения, мы смогли обрести уверенность в том, что такая связь действительно существует, и определить, что она может быть связана со структурами, известными как сломанные двугранные интервалы и экстремальные отражения. Обладая этими знаниями, профессор Уильямсон смог разработать удивительный и красивый алгоритм, который решит гипотезу о комбинаторной инвариантности. Мы вычислительно проверили новый алгоритм на более чем 3 миллионах примеров.

Вместе с профессором Лакенби и профессором Юхашем мы исследовали узлы — один из основных объектов изучения топологии. Узлы не только говорят нам о множестве способов запутывания веревки, но также имеют удивительную связь с квантовой теорией поля и неевклидовой геометрией. Алгебра, геометрия и квантовая теория разделяют уникальные точки зрения на эти объекты, и давняя загадка заключается в том, как соотносятся эти разные области: например, что геометрия узла говорит нам об алгебре? Мы обучили модель машинного обучения обнаруживать такой паттерн, и неожиданно выяснилось, что конкретная алгебраическая величина — сигнатура — напрямую связана с геометрией узла, которая ранее не была известна и не предполагалась существующей теорией. Используя методы атрибуции машинного обучения, мы помогли профессору Лакенби открыть новую величину, которую мы называем естественным наклоном, которая намекает на важный аспект структуры, который до сих пор упускали из виду. Вместе мы тогда смогли доказать точную природу взаимосвязи, установив некоторые из первых связей между этими различными разделами математики.

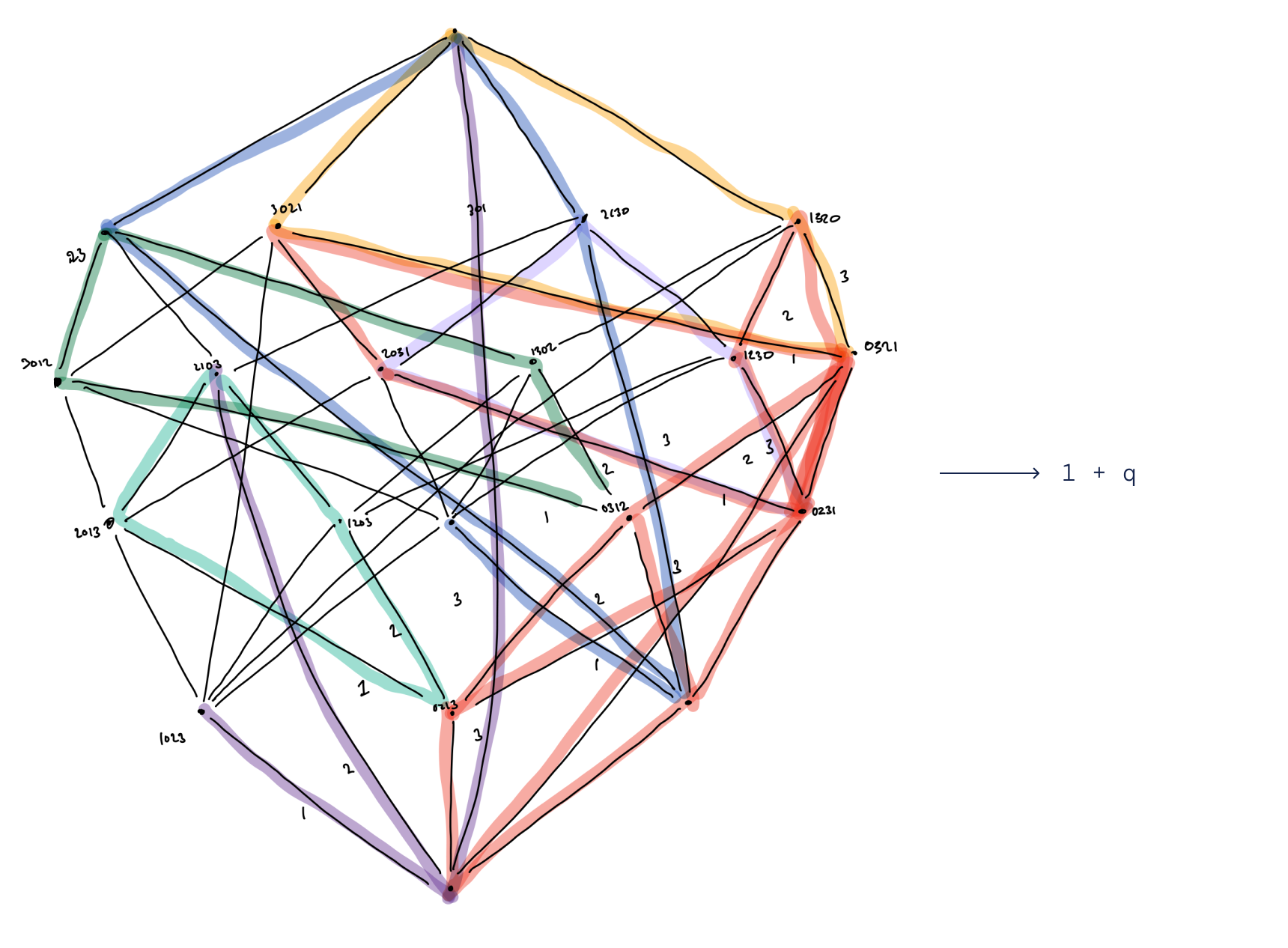
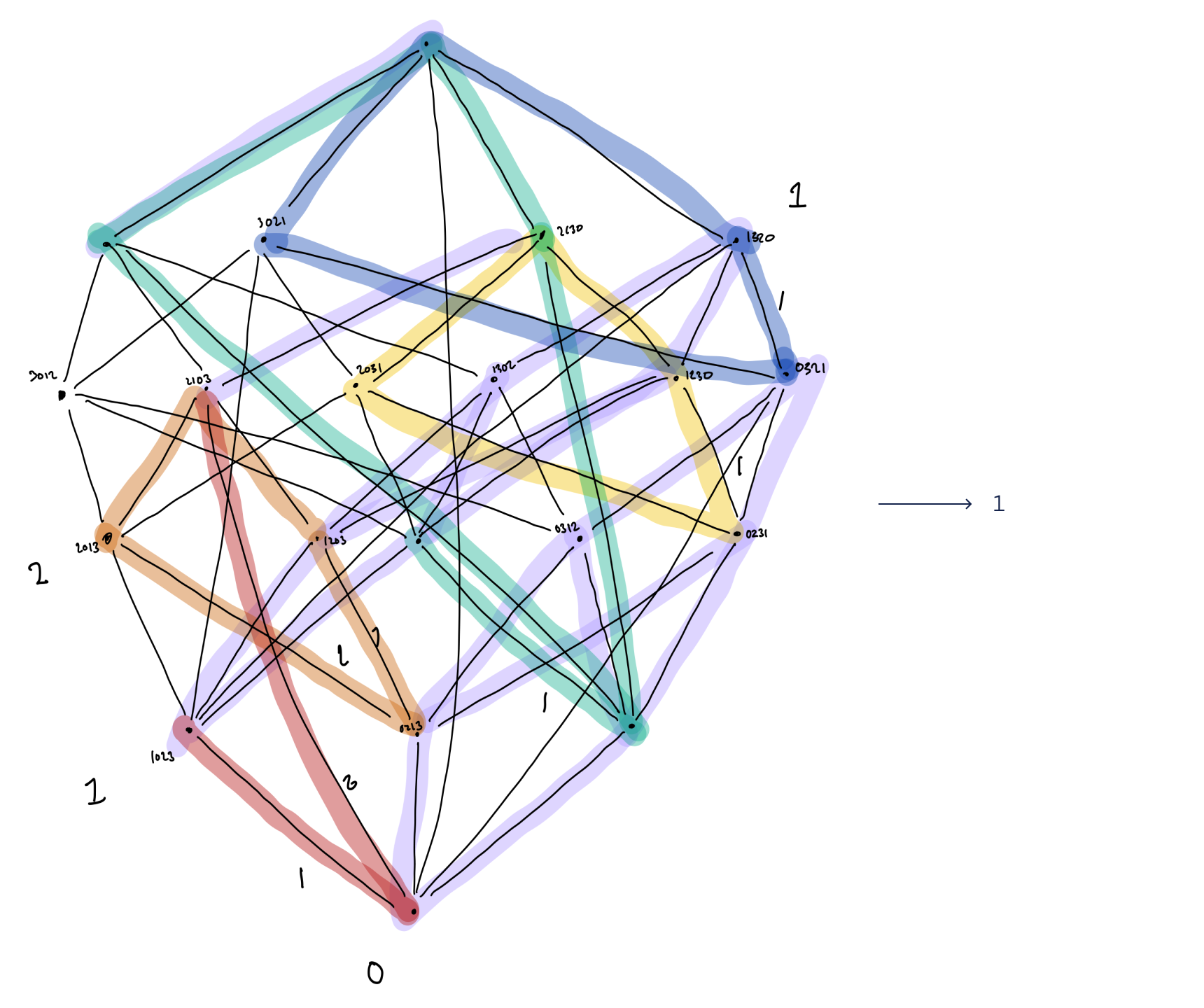
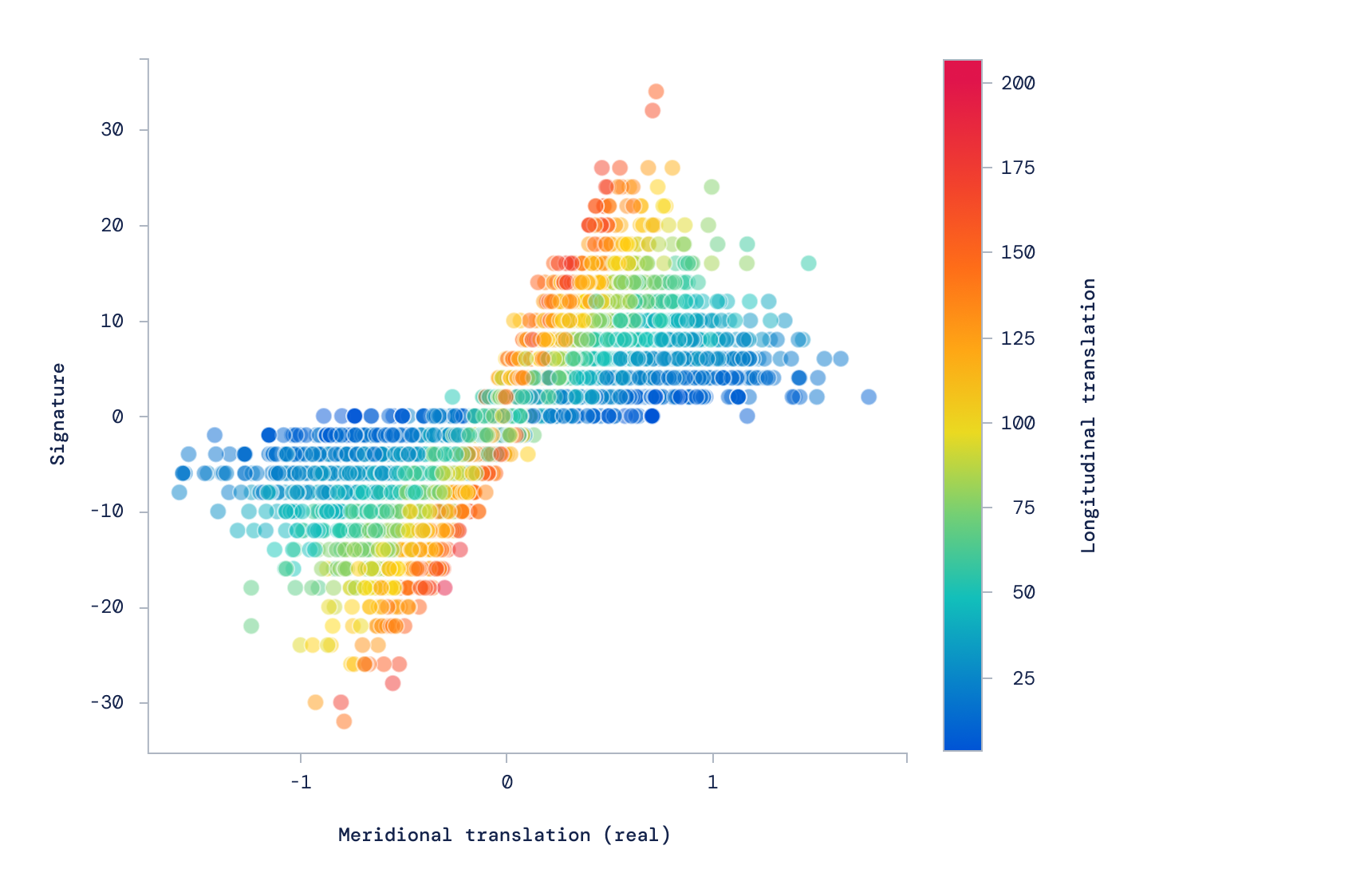
Использование методов обучения и систем искусственного интеллекта открывает большие перспективы для выявления и обнаружения закономерностей в математике. Мы надеемся, что даже если некоторые виды паттернов по-прежнему ускользают от современного машинного обучения. наша природа бумага может вдохновить других исследователей на рассмотрение потенциала ИИ как полезного инструмента в чистой математике. Чтобы воспроизвести результаты, любой может получить доступ к нашему интерактивные тетради. Размышляя о невероятном уме Рамануджана, Джордж Фредерик Джеймс Темпл писал: «Большие успехи в математике были достигнуты не логикой, а творческим воображением». Работая с математиками, мы с нетерпением ждем возможности увидеть, как ИИ может еще больше поднять красоту человеческой интуиции на новый уровень творчества.