Вознаграждение — это движущая сила агентов обучения с подкреплением (RL). Учитывая его центральную роль в RL, вознаграждение часто считается достаточно общим по своей экспрессивности, что резюмируется гипотезой вознаграждения Саттона и Литтмана:
«… все, что мы подразумеваем под целями и задачами, можно рассматривать как максимизацию ожидаемого значения кумулятивной суммы полученного скалярного сигнала (вознаграждения)».
– САТТОН (2004), ЛИТТМАН (2017)
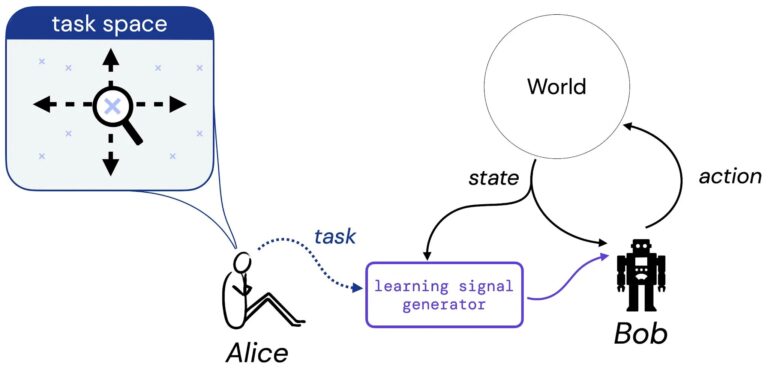
В нашей работе мы делаем первые шаги к систематическому изучению этой гипотезы. Для этого мы рассмотрим следующий мысленный эксперимент с участием Алисы, дизайнера, и Боба, обучающегося агента:
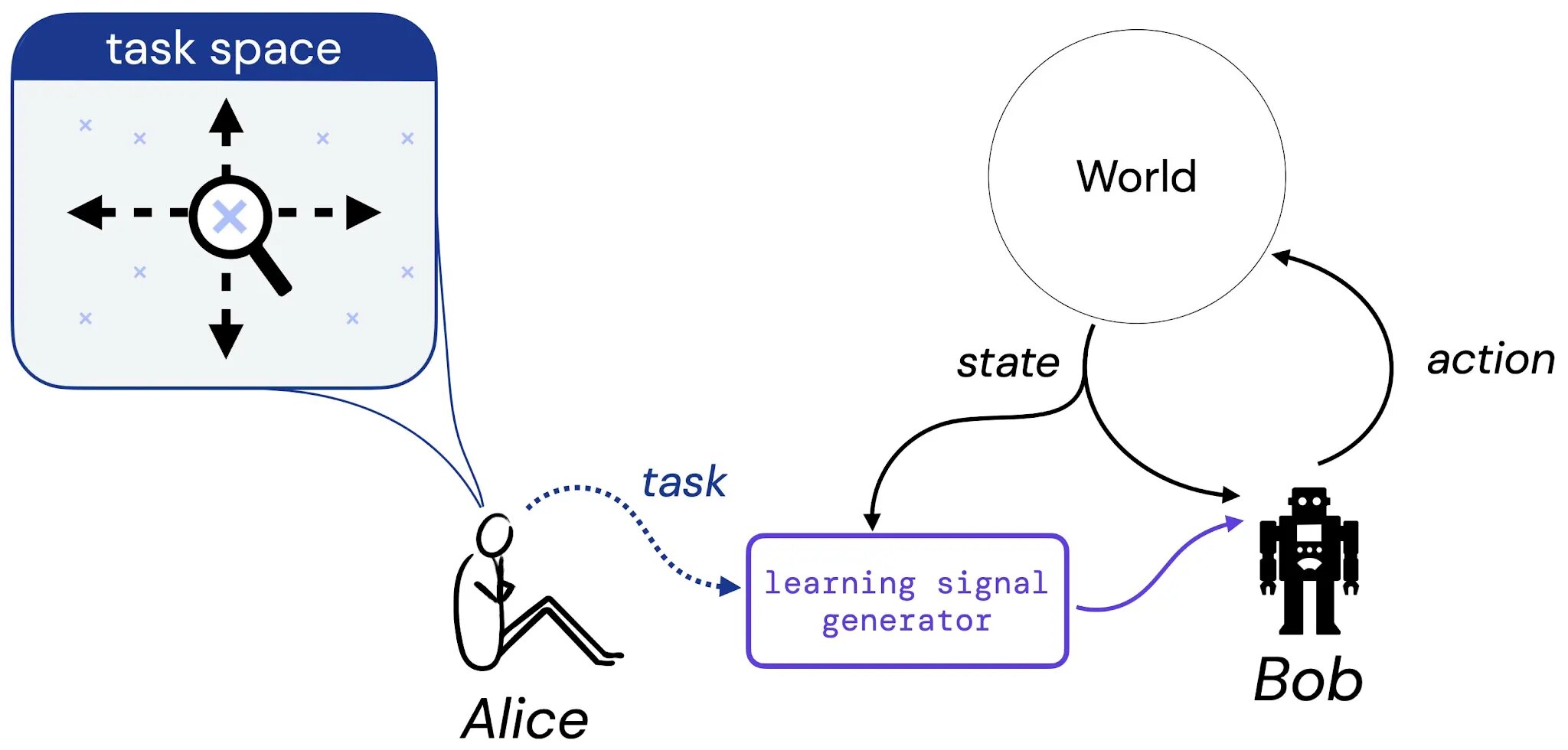
Мы предполагаем, что Алиса думает о задаче, которую, по ее мнению, должен научиться решать Боб, — эта задача может быть в форме описания на естественном языке («сбалансировать этот полюс»), воображаемого положения дел («достичь любой из выигрышных конфигураций шахматная доска») или что-то более традиционное, например функция вознаграждения или ценности. Затем мы представляем, что Алиса переводит свой выбор задачи в некий генератор, который подает сигнал обучения (например, награду) Бобу (агенту обучения), который будет учиться на этом сигнале на протяжении всей своей жизни. Затем мы обосновываем наше исследование гипотезы вознаграждения, ответив на следующий вопрос: если Алиса выбрала задачу, всегда ли существует функция вознаграждения, которая может передать эту задачу Бобу?
Что такое задача?
Чтобы сделать наше исследование этого вопроса конкретным, мы сначала сосредоточимся на трех видах задач. В частности, мы вводим три типа задач, которые, по нашему мнению, охватывают разумные типы задач: 1) набор приемлемых политик (SOAP), 2) порядок политики (PO) и 3) порядок траектории (TO). Эти три вида задач представляют собой конкретные примеры задач, которые мы могли бы захотеть, чтобы агент научился решать.
.jpg)
Затем мы изучаем, способно ли вознаграждение охватить каждый из этих типов задач в ограниченных средах. Важно отметить, что мы обращаем внимание только на марковские функции вознаграждения; например, при наличии пространства состояний, достаточного для формирования такой задачи, как пары (x,y) в мире сетки, существует ли функция вознаграждения, которая зависит только от того же самого пространства состояний, которое может захватить задачу?
Первый основной результат
Наш первый основной результат показывает, что для каждого из трех типов задач существуют пары среда-задача, для которых нет марковской функции вознаграждения, которая может зафиксировать задачу. Одним из примеров такой пары является задача «обойти всю сетку по часовой стрелке или против часовой стрелки» в типичном сеточном мире:
.jpg)
Эта задача естественным образом описывается протоколом SOAP, состоящим из двух допустимых политик: политики «по часовой стрелке» (синяя) и политики «против часовой стрелки» (фиолетовая). Чтобы марковская функция вознаграждения могла выразить эту задачу, необходимо было бы сделать эти две политики строго более ценными, чем все другие детерминированные политики. Однако такой марковской функции вознаграждения не существует: оптимальность единичного действия «движение по часовой стрелке» будет зависеть от того, двигался ли уже агент в этом направлении в прошлом. Поскольку функция вознаграждения должна быть марковской, она не может передавать такую информацию. Подобные примеры демонстрируют, что марковское вознаграждение не может охватывать каждый порядок политики и порядок траектории.
Второй основной результат
Учитывая, что некоторые задачи могут быть захвачены, а некоторые нет, мы затем исследуем, существует ли эффективная процедура для определения того, может ли данная задача быть захвачена с помощью вознаграждения в данной среде. Кроме того, если есть функция вознаграждения, которая охватывает данную задачу, в идеале мы хотели бы иметь возможность вывести такую функцию вознаграждения. Наш второй результат — положительный результат, который говорит, что для любой конечной пары среда-задача существует процедура, которая может 1) решить, может ли задача быть захвачена марковским вознаграждением в данной среде, и 2) вывести желаемую функцию вознаграждения, которая точно передает задачу, когда такая функция есть.
Эта работа устанавливает начальные пути к пониманию масштабов гипотезы вознаграждения, но еще многое предстоит сделать, чтобы обобщить эти результаты за пределы конечных сред, марковских вознаграждений и простых понятий «задачи» и «выразительности». Мы надеемся, что эта работа открывает новые концептуальные взгляды на вознаграждение и его место в обучении с подкреплением.