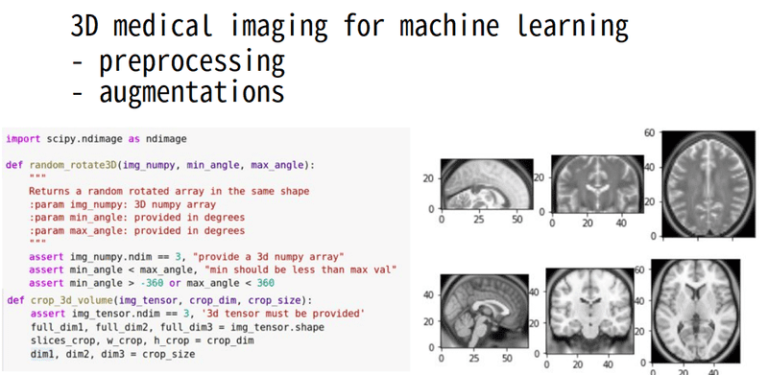
Когда я понял, что не могу применять обычные конвейеры обработки изображений к медицинским изображениям, я был полностью обескуражен. Почему такого функционала нет? Итак, я придумал этот пост (плюс блокнот) для отчаявшихся людей, которые, как и я, заинтересованы в решении проблем медицинской визуализации.
Мы уже обсудили сегментацию медицинских изображений и некоторые начальные сведения о системах координат и файлах DICOM. Мой опыт в этой области позволяет мне продолжать анализ данных, предварительную обработку и некоторые дополнения. Как я всегда говорю, если вы просто понимаете свои данные и их особенности, вы, вероятно, играете в бинго. В области медицинской визуализации я считаю, что некоторые манипуляции с данными, которые широко используются при предварительной обработке и дополнении в современных методах, имеют решающее значение для нашего понимания. С этой целью я предоставляю ноутбук для всех, чтобы поиграть. Он выполняет преобразования медицинских изображений, которые представляют собой просто структурированную трехмерную сетку.
Чтобы глубже погрузиться в то, как ИИ используется в медицине, вы не ошибетесь с ИИ для медицины онлайн-курс, предлагаемый Coursera. Если вы хотите сосредоточиться на анализе медицинских изображений с помощью глубокого обучения, я настоятельно рекомендую начать с Курс Udemy на основе Pytorch.
Данные: Мы будем играть с двумя изображениями МРТ, которые предоставлены nibabel (библиотека Python) для иллюстрации. Изображения хранятся в виде изящных файлов. Но перед этим давайте напишем код для визуализации трехмерных медицинских объемов.
Изображения будут показаны в 3 плоскостях: сагиттальной, коронарной и аксиальной, если смотреть слева направо на протяжении всего поста.
Визуализация двумерных плоскостей
На протяжении всего урока мы будем широко использовать функцию, которая визуализирует три срединных среза в сагиттальный, корональный и аксиальный самолетов соответственно. Напишем для этого минимальную функцию:
def show_mid_slice(img_numpy, title='img'):
"""
Accepts an 3D numpy array and shows median slices in all three planes
"""
assert img_numpy.ndim == 3
n_i, n_j, n_k = img_numpy.shape
center_i1 = int((n_i - 1) / 2)
center_j1 = int((n_j - 1) / 2)
center_k1 = int((n_k - 1) / 2)
show_slices((img_numpy(center_i1, :, :),
img_numpy(:, center_j1, :),
img_numpy(:, :, center_k1)))
plt.suptitle(title)
def show_slices(slices):
"""
Function to display a row of image slices
Input is a list of numpy 2D image slices
"""
fig, axes = plt.subplots(1, len(slices))
for i, slice in enumerate(slices):
axes(i).imshow(slice.T, cmap="gray", origin="lower")
Ничего больше, чем matplotlib “imshow" и манипуляции с массивом numpy. Для справки, медицинские изображения представляют собой один канал, и мы визуализируем их в оттенках серого.
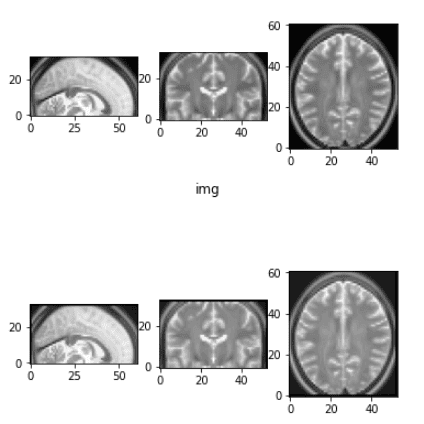
Два изображения, которые мы будем использовать для игры с множеством преобразований, можно проиллюстрировать ниже:
show_mid_slice(epi_img_numpy, 'first image')
show_mid_slice(anatomy_img_numpy,'second image')
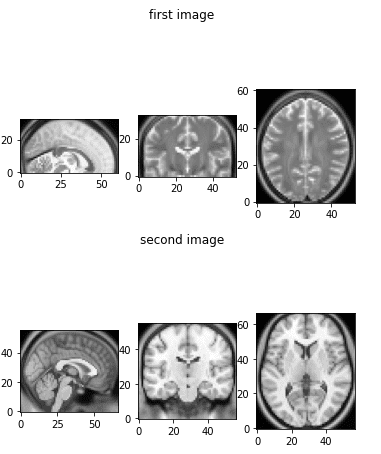
Исходные снимки МРТ головного мозга, которые мы будем использовать.
Теперь мы готовы идти! Начнем с изменения размера и масштабирования медицинских изображений. Да, это не совсем то же самое.
Изменение размера медицинского изображения (уменьшение/повышение дискретизации)
острый библиотека предоставляет множество функций для многомерных изображений. Поскольку медицинские изображения являются трехмерными, можно использовать множество функций. На этот раз мы будем использовать scipy.ndimage.interpolation.zoom для изменения размера изображения в желаемых размерах. Это похоже на понижение частоты дискретизации в 2D-изображении. Эту же функцию можно использовать для интерполяции для увеличения пространственных размеров. В качестве иллюстрации мы удвоим и уменьшим вдвое исходный размер изображения.
Имейте в виду, что при таком преобразовании обычно важно соблюдать соотношения.
Вы, наверное, не хотите потерять анатомию человеческого тела 🙂
import scipy
def resize_data_volume_by_scale(data, scale):
"""
Resize the data based on the provided scale
"""
scale_list = (scale,scale,scale)
return scipy.ndimage.interpolation.zoom(data, scale_list, order=0)
result = resize_data_volume_by_scale(epi_img_numpy, 0.5)
result2 = resize_data_volume_by_scale(epi_img_numpy, 2)
Такой вид масштабирования обычно называют изометрическим. Честно говоря, я не большой поклонник терминологии scipy, чтобы использовать слово масштабирование для этой функциональности.
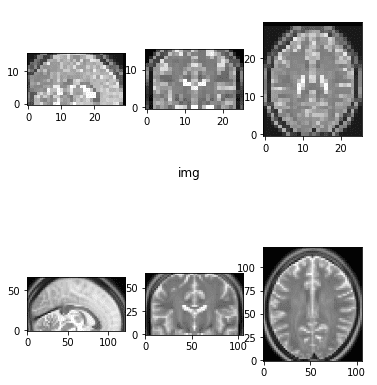
Изображение с пониженной и повышенной частотой дискретизации в 2 раза
Для тяжелого машинного обучения очень часто понижают разрешение изображения в более низком измерении.
Обратите внимание, что существует еще один тип изменения размера. Вместо предоставления желаемой выходной формы вы указываете желаемый размер вокселя (т.е. voxel_size=(1,1,1) мм). Nibabel предоставляет функцию resample_to_output(). Он работает с файлами nifti, а не с массивами numpy. Честно говоря, я бы не рекомендовал его в одиночку, так как полученные изображения могут иметь разную форму. Это может быть проблемой для глубокого обучения. Например, для создания пакетов с загрузчиками данных измерение должно быть одинаковым для всех экземпляров. Однако вы можете включить его на предыдущем этапе конвейера. Его можно использовать для приведения разных изображений к одинаковому или близкому размеру вокселя.
Масштабирование медицинских изображений (увеличение/уменьшение)
Масштабирование можно рассматривать как аффинное преобразование. Мы будем случайным образом увеличивать и уменьшать изображение. Это увеличение обычно помогает модели изучить масштабно-инвариантные функции.
def random_zoom(matrix,min_percentage=0.7, max_percentage=1.2):
z = np.random.sample() *(max_percentage-min_percentage) + min_percentage
zoom_matrix = np.array(((z, 0, 0, 0),
(0, z, 0, 0),
(0, 0, z, 0),
(0, 0, 0, 1)))
return ndimage.interpolation.affine_transform(matrix, zoom_matrix)
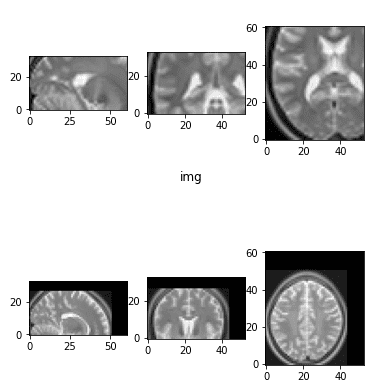
Случайное увеличение и уменьшение масштаба
Важно видеть, что пустая область заполнена черными пикселями (нулевой интенсивности).
Обратите внимание, что окружающий воздух на медицинских изображениях не имеет нулевой интенсивности. Черный действительно связан с медицинскими изображениями.
Следующим в списке является 3D-вращение.
Вращение медицинских изображений
Вращение — один из наиболее распространенных методов увеличения данных в компьютерном зрении. Это также считается методом самоконтроля с замечательными результатами (Спирос Гидарис и др. ).
В медицинской визуализации это аналогичная функциональность импорта, которая также использовалась при предварительном обучении с самоконтролем (Синьруи Чжуан и др. 2019 ). Простой случайный трехмерный поворот в заданном диапазоне градусов можно проиллюстрировать кодом ниже:
def random_rotate3D(img_numpy, min_angle, max_angle):
"""
Returns a random rotated array in the same shape
:param img_numpy: 3D numpy array
:param min_angle: in degrees
:param max_angle: in degrees
"""
assert img_numpy.ndim == 3, "provide a 3d numpy array"
assert min_angle < max_angle, "min should be less than max val"
assert min_angle > -360 or max_angle < 360
all_axes = ((1, 0), (1, 2), (0, 2))
angle = np.random.randint(low=min_angle, high=max_angle+1)
axes_random_id = np.random.randint(low=0, high=len(all_axes))
axes = all_axes(axes_random_id)
return scipy.ndimage.rotate(img_numpy, angle, axes=axes)
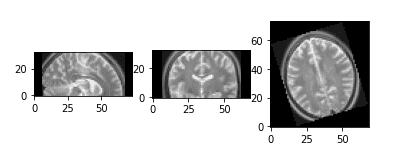
Случайное 3D-вращение
Нам просто нужно определить ось и угол поворота. Поскольку масштабирование предоставило модели больше разнообразия для изучения инвариантных к масштабу функций, вращение помогает в изучении инвариантных к вращению функций.
Следующим в нашем списке является переворачивание изображений.
Переворот медицинского изображения
Подобно обычным изображениям RGB, мы можем выполнять переворот оси в медицинских изображениях. На данный момент очень важно прояснить одну вещь:
Когда мы выполняем дополнения и/или предварительную обработку наших данных, нам, возможно, придется применить аналогичные операции к данным наземной достоверности.
Например, если мы решаем задачу сегментации медицинских изображений, важно перевернуть карту целевой сегментации. Простую реализацию можно найти ниже:
def random_flip(img, label=None):
axes = (0, 1, 2)
rand = np.random.randint(0, 3)
img = flip_axis(img, axes(rand))
img = np.squeeze(img)
if label is None:
return img
else:
y = flip_axis(y, axes(rand))
y = np.squeeze(y)
return x, y
def flip_axis(x, axis):
x = np.asarray(x).swapaxes(axis, 0)
x = x(::-1, ...)
x = x.swapaxes(0, axis)
return x
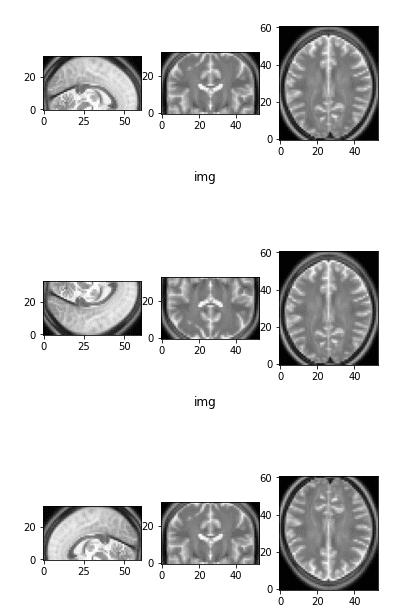
Исходное изображение в качестве эталона и две перевернутые версии
Обратите внимание, что при повороте одной оси меняются два вида. Первое изображение сверху является исходным изображением в качестве эталона.
Медицинское смещение изображения (смещение)
Здесь я хотел бы рассказать о другом.
Вращение, смещение и масштабирование — не что иное, как аффинные преобразования.
Иногда я реализую их, просто определяя аффинные преобразования и применяя их к изображению с помощью scipy, а иногда использую уже реализованные функции для многомерной обработки изображений.
Чтобы использовать эту операцию в моем конвейере увеличения данных, вы можете видеть, что я включил функцию-оболочку. Последний в основном выбирает случайное число, обычно в желаемом диапазоне, и вызывает функцию аффинного преобразования. Ниже приведена реализация для случайного смещения/смещения.
def transform_matrix_offset_center_3d(matrix, x, y, z):
offset_matrix = np.array(((1, 0, 0, x), (0, 1, 0, y), (0, 0, 1, z), (0, 0, 0, 1)))
return ndimage.interpolation.affine_transform(matrix, offset_matrix)
def random_shift(img_numpy, max_percentage=0.4):
dim1, dim2, dim3 = img_numpy.shape
m1,m2,m3 = int(dim1*max_percentage/2),int(dim1*max_percentage/2), int(dim1*max_percentage/2)
d1 = np.random.randint(-m1,m1)
d2 = np.random.randint(-m2,m2)
d3 = np.random.randint(-m3,m3)
return transform_matrix_offset_center_3d(img_numpy, d1, d2, d3)
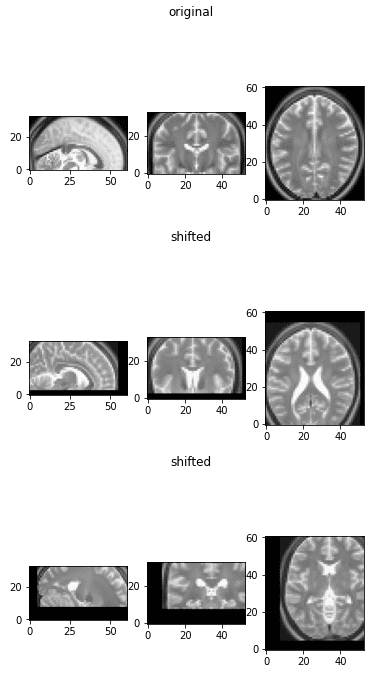
Смещенные медицинские изображения
Эта аугментация не очень распространена в аугментации медицинских изображений, но мы включили их сюда для полноты картины.
Причина, по которой мы ее не включаем, заключается в том, что сверточные нейронные сети по определению предназначены для изучения свойств, инвариантных к трансляции.
Случайная 3D-обрезка
Обрезка также не сильно отличается от естественных изображений. Однако имейте в виду, что обычно нам приходится брать все срезы измерения, и нам нужно позаботиться об этом. Причина в том, что одно измерение может иметь меньше срезов, чем другие. Например, однажды мне пришлось иметь дело с изображением размером 384x384x64, которое часто встречается в КТ-изображения.
def crop_3d_volume(img_tensor, crop_dim, crop_size):
assert img_tensor.ndim == 3, '3d tensor must be provided'
full_dim1, full_dim2, full_dim3 = img_tensor.shape
slices_crop, w_crop, h_crop = crop_dim
dim1, dim2, dim3 = crop_size
if full_dim1 == dim1:
img_tensor = img_tensor(:, w_crop:w_crop + dim2,
h_crop:h_crop + dim3)
elif full_dim2 == dim2:
img_tensor = img_tensor(slices_crop:slices_crop + dim1, :,
h_crop:h_crop + dim3)
elif full_dim3 == dim3:
img_tensor = img_tensor(slices_crop:slices_crop + dim1, w_crop:w_crop + dim2, :)
else:
img_tensor = img_tensor(slices_crop:slices_crop + dim1, w_crop:w_crop + dim2,
h_crop:h_crop + dim3)
return img_tensor
def find_random_crop_dim(full_vol_dim, crop_size):
assert full_vol_dim(0) >= crop_size(0), "crop size is too big"
assert full_vol_dim(1) >= crop_size(1), "crop size is too big"
assert full_vol_dim(2) >= crop_size(2), "crop size is too big"
if full_vol_dim(0) == crop_size(0):
slices = crop_size(0)
else:
slices = np.random.randint(full_vol_dim(0) - crop_size(0))
if full_vol_dim(1) == crop_size(1):
w_crop = crop_size(1)
else:
w_crop = np.random.randint(full_vol_dim(1) - crop_size(1))
if full_vol_dim(2) == crop_size(2):
h_crop = crop_size(2)
else:
h_crop = np.random.randint(full_vol_dim(2) - crop_size(2))
return (slices, w_crop, h_crop)
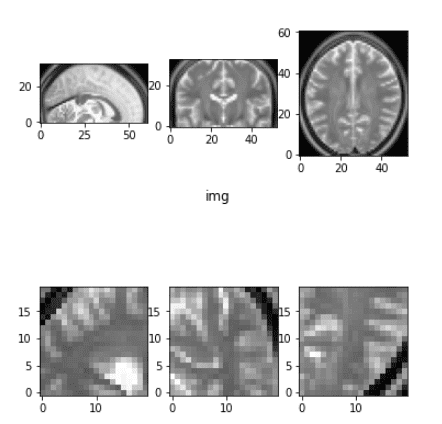
Пример случайной обрезки
Существуют и другие методы обрезки, которые фокусируются на интересующей нас области, например на опухоли, но мы не будем сейчас в них углубляться.
До сих пор мы играли с геометрическими преобразованиями. Давайте посмотрим, что мы можем сделать с интенсивностью изображения.
Значения интенсивности клипа (выбросы)
Этот шаг неприменим для этого урока, но в целом он может оказаться весьма полезным. Особенно для КТ-изображения. Причина, по которой это неприменимо, заключается в том, что изображения МРТ находятся в довольно узком диапазоне значений.
def percentile_clip(img_numpy, min_val=5, max_val=95):
"""
Intensity normalization based on percentile
Clips the range based on the quartile values.
:param min_val: should be in the range (0,100)
:param max_val: should be in the range (0,100)
:return: intensity normalized image
"""
low = np.percentile(img_numpy, min_val)
high = np.percentile(img_numpy, max_val)
img_numpy(img_numpy < low) = low
img_numpy(img_numpy > high) = high
return img_numpy
def clip_range(img_numpy, min_intensity=10, max_intensity=240):
return np.clip(img_numpy, min_intensity, max_intensity)
Нормализация интенсивности в медицинских изображениях
Здесь я включаю наиболее распространенные нормализации интенсивности: минимум-максимум и среднее/стандартное значение. Следует иметь в виду одну маленькую вещь:
Когда мы выполняем нормализацию среднего/стандартного значения, мы обычно опускаем воксели с нулевой интенсивностью при расчете среднего. Это справедливо в основном для изображений МРТ.
Один из способов взглянуть на это, если у нас есть изображение мозга; мы, вероятно, не хотим нормализовать его с интенсивностью вокселей вокруг него.
def normalize_intensity(img_tensor, normalization="mean"):
"""
Accepts an image tensor and normalizes it
:param normalization: choices = "max", "mean" , type=str
For mean normalization we use the non zero voxels only.
"""
if normalization == "mean":
mask = img_tensor.ne(0.0)
desired = img_tensor(mask)
mean_val, std_val = desired.mean(), desired.std()
img_tensor = (img_tensor - mean_val) / std_val
elif normalization == "max":
MAX, MIN = img_tensor.max(), img_tensor.min()
img_tensor = (img_tensor - MIN) / (MAX - MIN)
return img_tensor
Нет смысла визуализировать это преобразование, поскольку его цель — передать предварительно обработанные данные в модель глубокого обучения. Конечно, любой другой вид нормализации интенсивности может применяться к медицинским изображениям.
Упругая деформация
Когда я впервые прочитал это преобразование в оригинальной статье Unet, я не понял ни единого слова из абзаца:
«Что касается наших задач, то доступных обучающих данных очень мало, мы используем избыточную аугментацию данных, применяя упругие деформации к имеющимся обучающим изображениям. Это позволяет сети научиться инвариантности к таким деформациям без необходимости видеть эти преобразования в аннотированном корпусе изображений. Это особенно важно в биомедицинской сегментации, поскольку деформация раньше была наиболее распространенным изменением ткани, и реалистичные деформации можно эффективно моделировать» ~ Олаф Роннебергер и др. 2015 (бумага Unet)
Честно говоря, я не заглядывал в оригинальную публикацию 2003 года. И вы, вероятно, тоже не будете. Я изучил некоторые другие реализации кода и попытался сделать его более простым. Я решил включить его в свой учебник, потому что вы часто встретите его в литературе.
def elastic_transform_3d(image, labels=None, alpha=4, sigma=35, bg_val=0.1):
"""
Elastic deformation of images as described in
Simard, Steinkraus and Platt, "Best Practices for
Convolutional Neural Networks applied to Visual
Document Analysis", in
Proc. of the International Conference on Document Analysis and
Recognition, 2003.
Modified from:
https://gist.github.com/chsasank/4d8f68caf01f041a6453e67fb30f8f5a
https://github.com/fcalvet/image_tools/blob/master/image_augmentation.py#L62
Modified to take 3D inputs
Deforms both the image and corresponding label file
image linear/trilinear interpolated
Label volumes nearest neighbour interpolated
"""
assert image.ndim == 3
shape = image.shape
dtype = image.dtype
coords = np.arange(shape(0)), np.arange(shape(1)), np.arange(shape(2))
im_intrps = RegularGridInterpolator(coords, image,
method="linear",
bounds_error=False,
fill_value=bg_val)
dx = gaussian_filter((np.random.rand(*shape) * 2 - 1), sigma,
mode="constant", cval=0.) * alpha
dy = gaussian_filter((np.random.rand(*shape) * 2 - 1), sigma,
mode="constant", cval=0.) * alpha
dz = gaussian_filter((np.random.rand(*shape) * 2 - 1), sigma,
mode="constant", cval=0.) * alpha
x, y, z = np.mgrid(0:shape(0), 0:shape(1), 0:shape(2))
indices = np.reshape(x + dx, (-1, 1)), \
np.reshape(y + dy, (-1, 1)), \
np.reshape(z + dz, (-1, 1))
image = np.empty(shape=image.shape, dtype=dtype)
image = im_intrps(indices).reshape(shape)
if labels is not None:
lab_intrp = RegularGridInterpolator(coords, labels,
method="nearest",
bounds_error=False,
fill_value=0)
labels = lab_intrp(indices).reshape(shape).astype(labels.dtype)
return image, labels
return image
До и после упругой деформации
Вам нужно иметь в виду, что это преобразование изменяет интенсивность и применяет некоторый гауссовский шум в каждом измерении. Для получения дополнительной информации вы должны вернуться к оригиналу работа.
Заключение
К настоящему времени вы можете понять мои мысли об особенностях предварительной обработки и дополнений медицинских изображений. Но не забывайте: вы можете играть с учебник онлайн и увидеть преобразования самостоятельно. Помогает, поверьте. Понимание наших медицинских изображений очень важно. Теперь вы можете выбрать, какие преобразования применить в вашем проекте.
Если вам понравился наш урок, не стесняйтесь поделиться им на своей странице в социальных сетях в качестве награды за нашу работу. Было бы весьма признателен.
Оставайтесь с нами, чтобы не пропустить новые летние статьи об искусственном интеллекте!
* Раскрытие информации: Обратите внимание, что некоторые из приведенных выше ссылок могут быть партнерскими ссылками, и без дополнительной оплаты для вас мы будем получать комиссию, если вы решите совершить покупку после перехода по ссылке.