Это совместный пост с Инбар Наор. Первоначально опубликовано на Engineering.taboola.com.

В первый пост В этой серии мы обсудили три типа неопределенности, которые могут повлиять на вашу модель, — неопределенность данных, неопределенность модели и неопределенность измерений. В второй пост мы говорили о различных методах обработки неопределенности модели. Тогда в нашем третий пост
мы показали, как можно использовать неопределенность модели для поощрения изучения новых элементов в рекомендательных системах.

Разве не было бы здорово, если бы мы могли принципиально обрабатывать все три типа неопределенности, используя одну унифицированную модель? В этом посте мы покажем вам, как мы в Taboola реализовали нейронную сеть, которая оценивает как вероятность релевантности элемента пользователю, так и неопределенность этого прогноза.

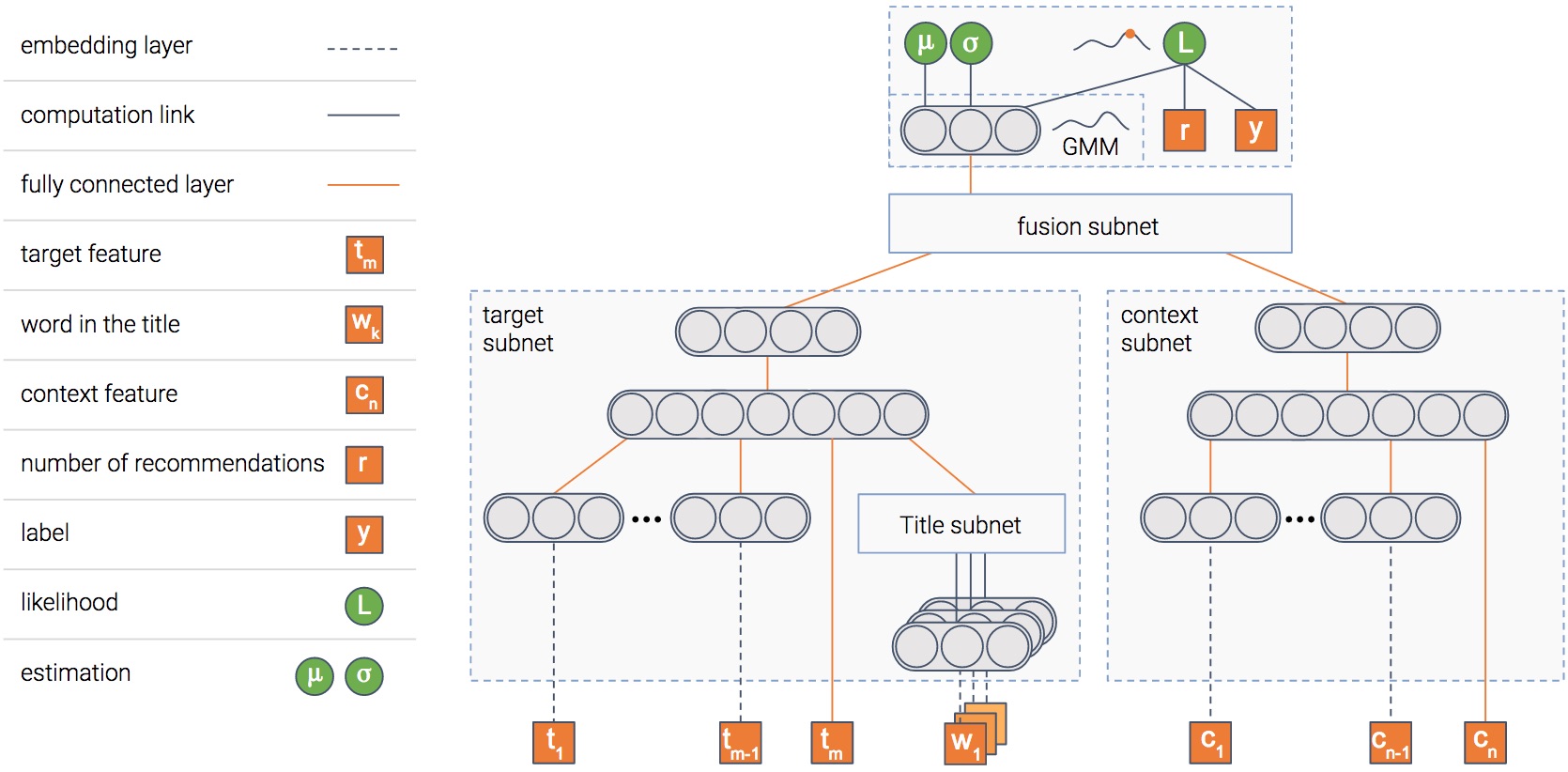
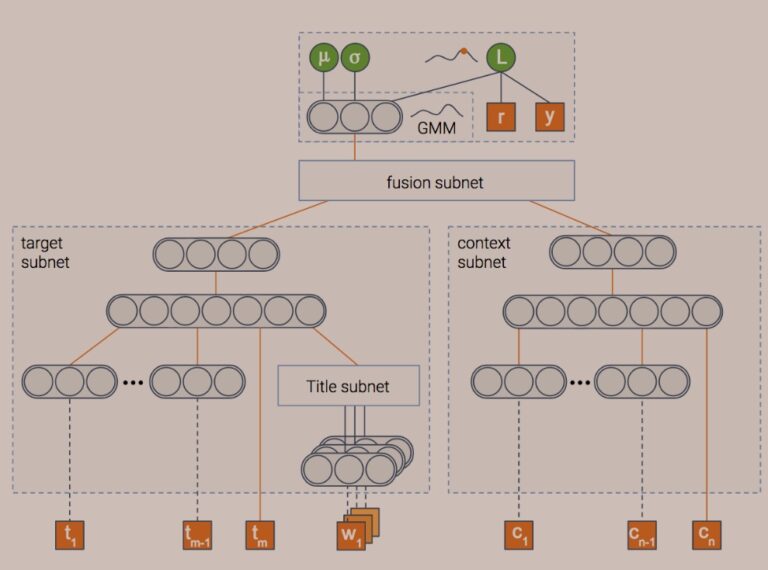
Картинка стоит тысячи слов, не так ли? А картинка, содержащая тысячу нейронов?…

В любом случае, это модель, которую мы используем. Модель состоит из нескольких модулей. Объясним цель каждого из них, и тогда картина прояснится…

Модуль элемента

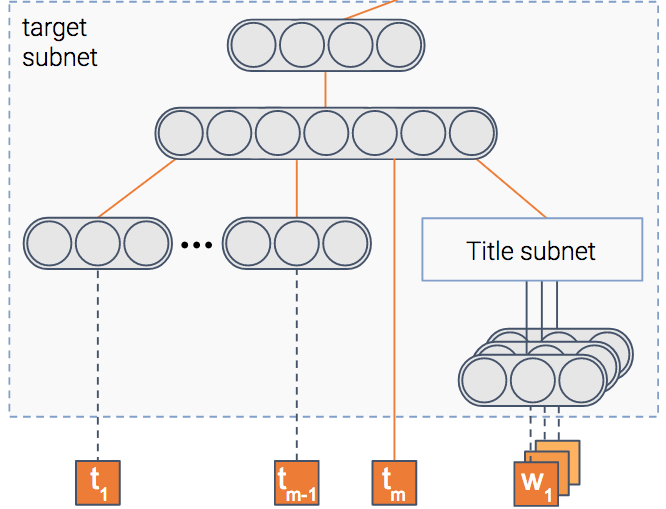
Модель пытается предсказать вероятность клика по элементу, т. е. — CTR (Click Through Rate). Для этого у нас есть модуль, который получает в качестве входных данных характеристики элемента, такие как его заголовок и эскиз, и выводит плотное представление — вектор чисел, если хотите.

После обучения модели этот вектор будет содержать важную информацию, извлеченную из элемента.

Контекстный модуль

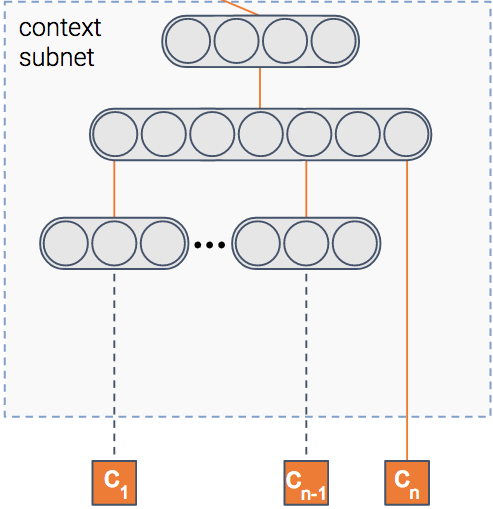
Мы сказали, что модель предсказывает вероятность клика по элементу, верно? Но в каком контексте показан предмет?

Контекст может означать многое — издатель, пользователь, время суток и т. д. Этот модуль получает в качестве входных данных характеристики контекста. Затем он выводит плотное представление контекста.

Fusion модуль

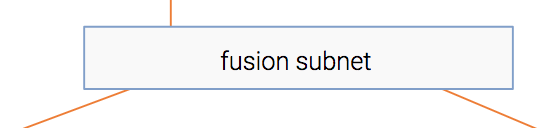
Таким образом, у нас есть информация, извлеченная как из элемента, так и из контекста. Наверняка между ними есть какое-то взаимодействие. Например, статья о футболе, скорее всего, будет иметь более высокий CTR в спортивном издательстве, чем в финансовом.

Этот модуль объединяет два представления в одно аналогично совместной фильтрации.

Модуль оценки

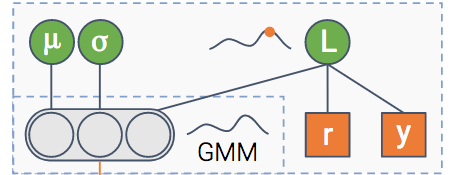
В конце у нас есть модуль, целью которого является прогнозирование CTR. Кроме того, он также оценивает неопределенность оценки CTR.

Я думаю, вы в основном не уверены в том, как этот модуль работает, так что давайте прольем на него свет.

Мы познакомим вас с тремя типами неопределенности, которые мы упомянули, и покажем, как каждая из них обрабатывается нашей моделью. Во-первых, давайте рассмотрим неопределенность данных.

Давайте возьмем некоторую общую нейронную сеть, обученную задаче регрессии. Одной из распространенных функций потерь является MSE — среднеквадратическая ошибка. Нам нравится эта потеря, потому что она интуитивно понятна, верно? Вы хотите минимизировать ошибки… Но оказывается, что когда вы минимизируете MSE, вы неявно максимизируете вероятность данных — предполагая, что метка распределяется нормально с фиксированным стандартным отклонением \(\сигма\). Этот \(\сигма\) шум, присущий данным.

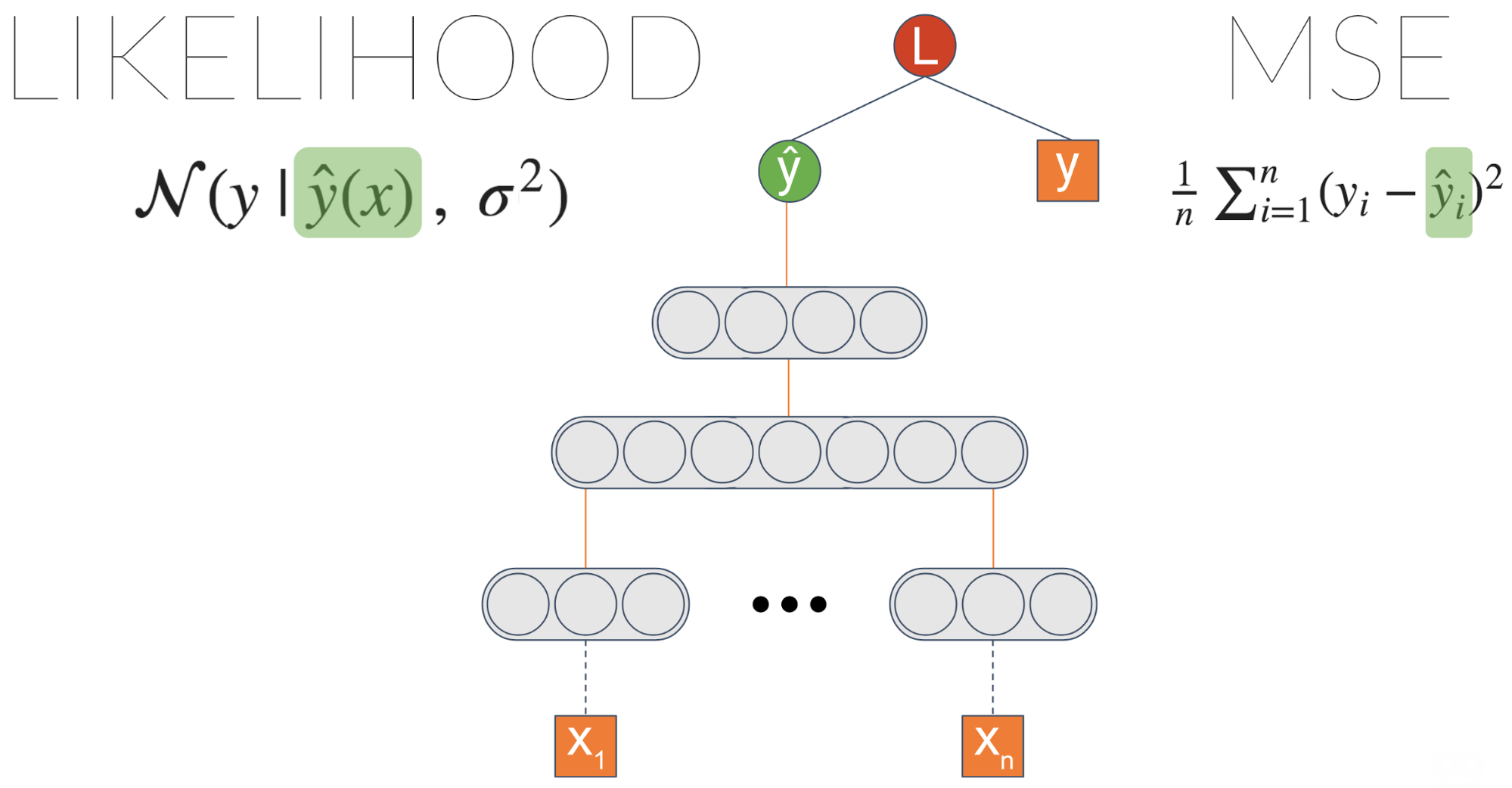
Одна вещь, которую мы можем сделать, это явно максимизировать вероятность, введя новый узел, который мы назовем \(\сигма\). Подключив его к уравнению правдоподобия и позволив градиентам распространяться, этот узел научится выводить шум данных.

Мы не добились ничего другого, верно? Мы получили результат, эквивалентный исходной модели на основе MSE. Однако теперь мы можем ввести ссылку с последнего слоя на \(\сигма\):

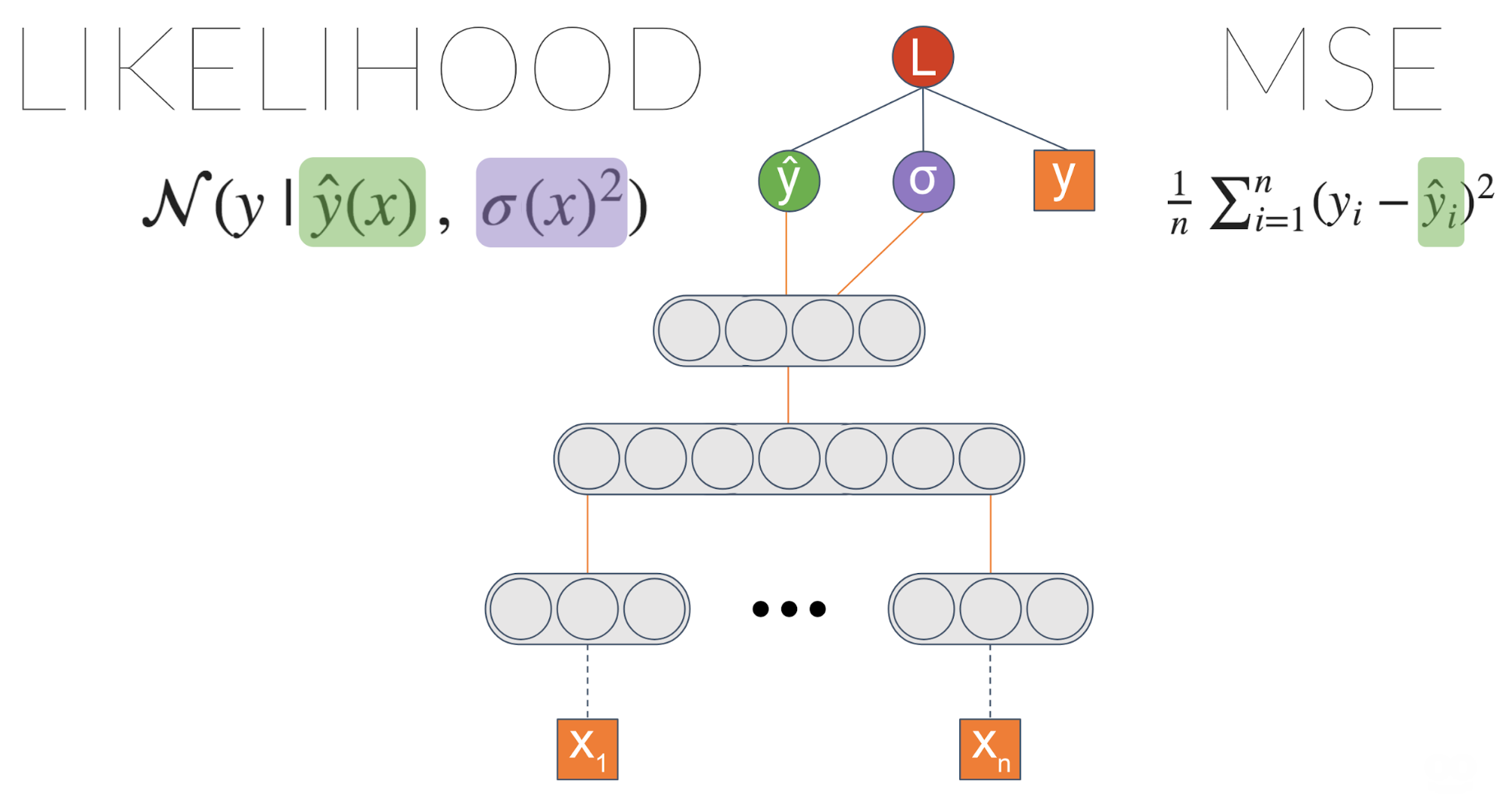
Теперь мы переходим к чему-то интересному! \(\сигма\) теперь является функцией ввода. Это означает, что модель может научиться связывать разные уровни неопределенности данных с разными входными данными.

Мы можем сделать модель еще мощнее. Вместо оценки гауссовского распределения мы можем оценить смесь гауссиан. Чем больше гауссианов мы добавим в микс, тем больше будет емкость у модели — и она будет более склонна к переобучению, так что будьте осторожны с этим.

Эта архитектура называется MDN — Mixture Density Network. Он был представлен
Бишоп и др. в 1994 году. Вот пример того, что он захватывает:

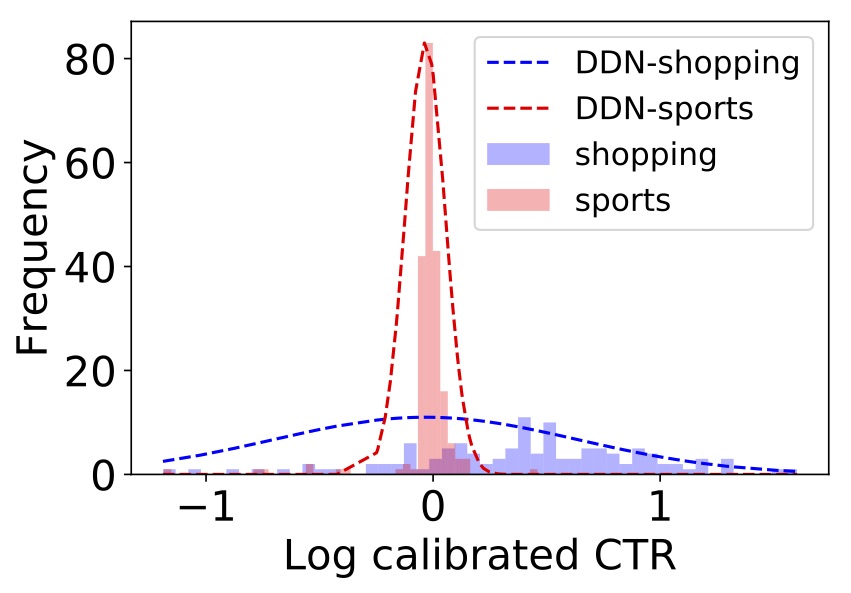
У нас есть две группы похожих предметов — одна о покупках, другая о спорте.

Оказывается, товары для покупок, как правило, имеют более изменчивый CTR — возможно, из-за модности. Действительно, если мы попросим модель оценить неопределенность одного элемента в каждой группе (пунктирный график на рисунке), мы получим более высокую неопределенность для покупок по сравнению со спортом.

Так что неопределенность данных позади. Что дальше?

Этот немного сложнее. В первый пост мы объяснили, что иногда измерения могут быть шумными. Это может привести к зашумленным функциям или даже зашумленным меткам. В нашем случае наша метка \(у\) — это эмпирический CTR элемента — количество кликов по нему, деленное на количество показов.

Допустим, истинный CTR элемента \(у^*\) — то есть без шума измерений. Это был бы CTR, если бы мы показывали элемент бесконечное количество раз в контексте. Но время конечно (по крайней мере, то время, которое у нас есть), поэтому мы показывали его только конечное количество раз. Мы измерили наблюдаемый CTR \(у\). Этот \(у\) имеет измерительный шум, который мы обозначаем как \(\эпсилон\).

Далее мы предполагаем \(\эпсилон\) нормально распределяется с \(\сигма_\эпсилон\) как стандартное отклонение. \(\сигма_\эпсилон\) функция \(р\) — сколько раз мы показывали товар. Больший \(р\) есть, чем меньше \(\сигма_\эпсилон\) получает, что делает \(у\) больше похоже на \(у^*\).

В конце концов, после того как мы избавим вас от математических подробностей (которые вы можете найти в нашей газете), мы получаем это уравнение правдоподобия:

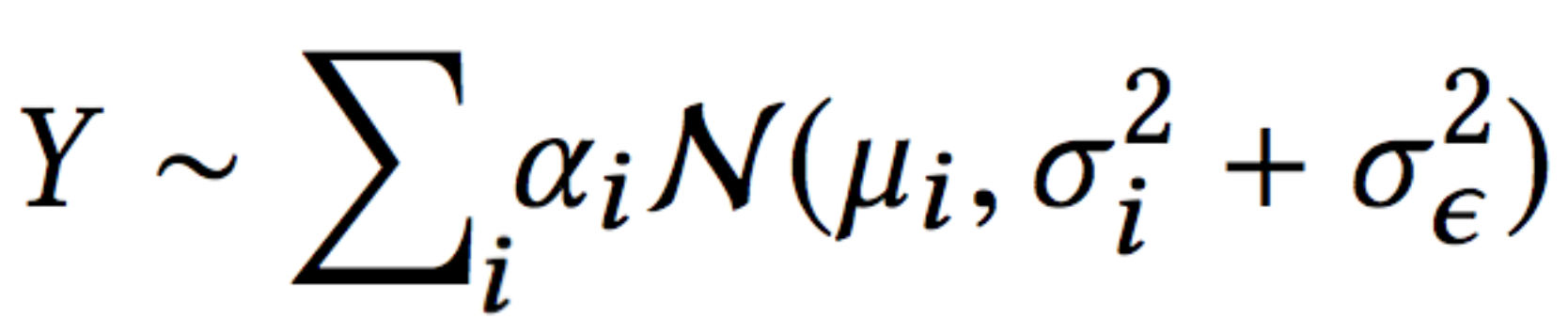
Это то же самое, что и вероятность, которую мы имеем в архитектуре MDN смеси гауссианов, с одним отличием — член ошибки делится на два:

• неопределенность данных (\(\sigma_i\))
• погрешность измерения (\(\сигма_\эпсилон\))

Теперь, когда модель может объяснить каждую неопределенность, используя разные термины, неопределенность данных не загрязняется неопределенностью измерения.

Помимо возможности лучше объяснять данные, это позволяет нам использовать больше данных в процессе обучения. Это связано с тем, что перед этой работой мы отфильтровали данные со слишком большим количеством шума.

В предыдущем посте мы обсуждали, как справляться с неопределенностью модели. Один из подходов, которые мы описали, заключался в использовании исключения во время вывода.

Возможность оценить неопределенность модели позволяет нам лучше понять, чего модель не знает из-за отсутствия данных. Итак, давайте проверим это!

Давайте посмотрим, связаны ли уникальные заголовки с высокой неопределенностью. Мы сопоставим каждый заголовок в обучающем наборе с плотным представлением (например, средние вложения word2vec) и ожидаем, что модель будет менее уверенной в отношении уникальных заголовков — заголовков, которые отображаются в разреженные области пространства встраивания.

Чтобы проверить это, мы рассчитали разреженные и плотные области, вычислив KDE (оценка плотности ядра). Это метод оценки PDF (функции плотности вероятности) нашего пространства. Затем мы попросили модель оценить неопределенность, связанную с каждым заголовком. Оказывается, модель действительно имеет более высокую неопределенность в разреженных областях!

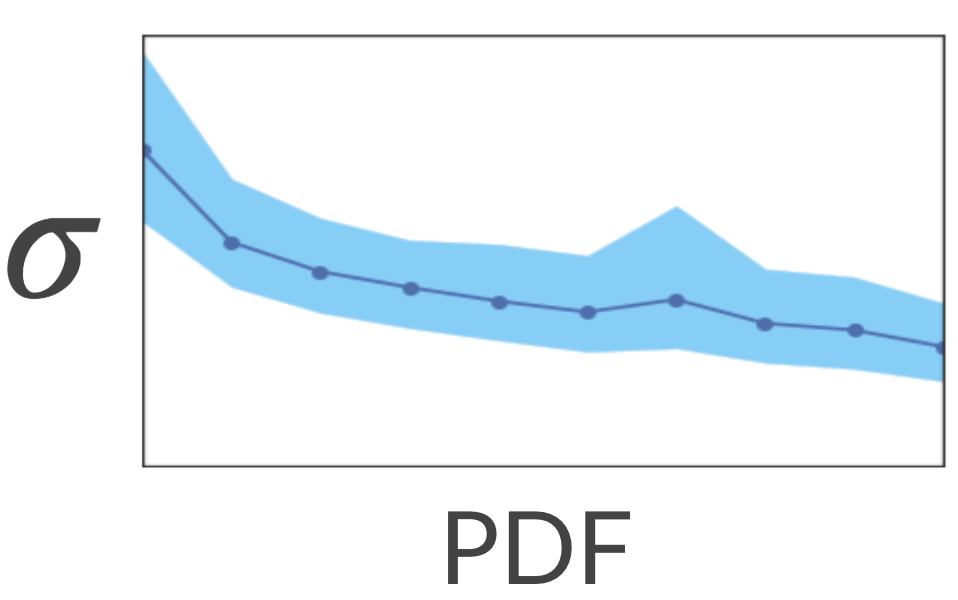
Хорошо… Что произойдет, если мы покажем модели больше заголовков из разреженных регионов? Будет ли он более определенным в отношении этих регионов? Давайте проверим это!

Мы взяли кучу похожих названий про автомобили и убрали их из обучающей выборки. По сути, это изменило их область в пространстве с плотной на разреженную. Затем мы оценили неопределенность модели для этих заголовков. Как и ожидалось, неопределенность была высокой.

Наконец, мы добавили в обучающую выборку только одно из названий и переобучили модель. К нашему удовлетворению, теперь неопределенность уменьшилась на все из этих предметов. Аккуратный!

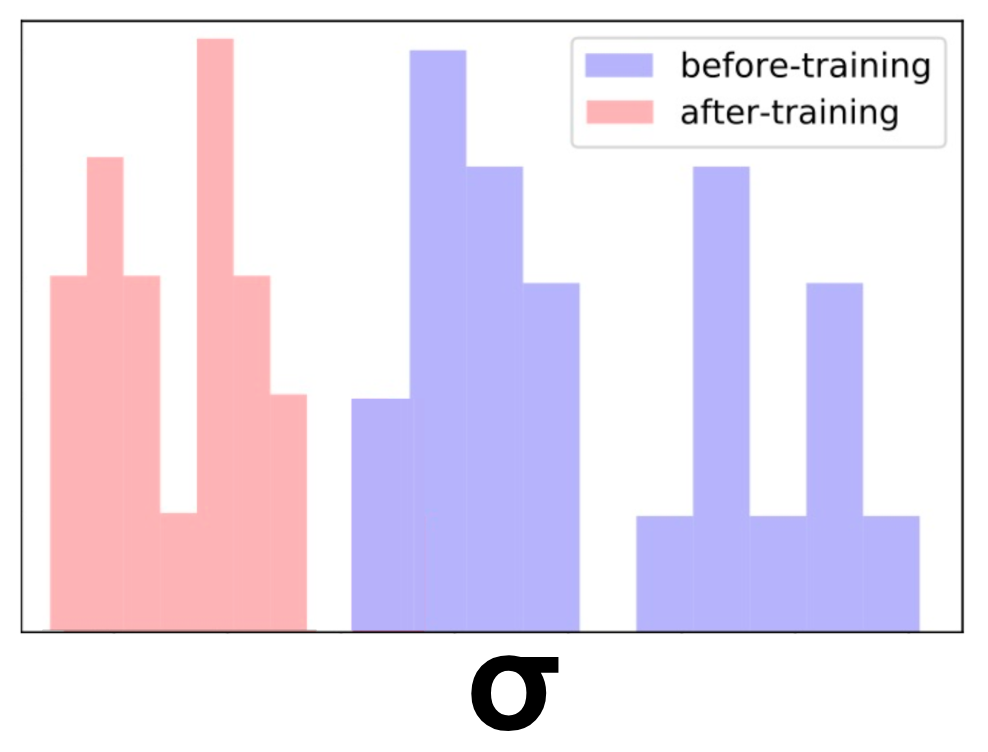
Как мы видели в пост о разведке-эксплуатации, мы можем поощрять исследование этих редких регионов. После этого неопределенность уменьшится. Это приведет к естественному упадку исследования этого региона.

В этом посте мы подробно рассказали о том, как мы моделируем все три типа неопределенности — данные, модель и измерение — принципиальным образом, используя одну унифицированную модель.

Мы рекомендуем вам подумать, как вы можете использовать неопределенность в своем приложении! Даже если вам не нужно явно моделировать неопределенность в своем прогнозе, вы можете использовать ее в процессе обучения — если ваша модель сможет лучше понять, как генерируются данные и как неопределенность влияет на игру, ее можно улучшить.

Это четвертый пост из серии статей, которые мы представляем на семинаре конференции KDD в этом году: сети с высокой плотностью и неопределенность в рекомендательных системах.

Первый пост можно найти здесь.

Второй пост можно найти здесь.

Третий пост можно найти здесь.

Первоначально опубликовано на
Engineering.taboola.com
мной и Инбар Наор.