
За последние пару лет глубокое обучение (ГО) стало основным инструментом для приложений во многих областях, таких как зрение, НЛП, аудио, данные потока кликов и т. д. Недавно исследователи начали успешно применять методы глубокого обучения для графических наборов данных в таких областях, как социальные сети. сети, рекомендательные системы и биология, где данные изначально структурированы графически.
Так как же работают графовые нейронные сети? Зачем они нам нужны?
В задачах машинного обучения, связанных с графическими данными, мы обычно хотим описать каждый узел в графе таким образом, чтобы мы могли передать его в какой-либо алгоритм машинного обучения. Без DL пришлось бы вручную извлекать характеристики, такие как количество соседей узла. Но это кропотливая работа.
Вот где DL сияет. Он автоматически использует структуру графа для извлечения признаков для каждого узла. Эти функции называются вложениями.
Интересно то, что даже если у вас нет абсолютно никакой информации об узлах, вы все равно можете использовать DL для извлечения вложений. Структура графа, то есть шаблоны связности, содержат полезную информацию.
Итак, как мы можем использовать структуру для извлечения информации? Может ли нам действительно помочь контекст каждого узла в графе?
Одним из хорошо известных алгоритмов, который извлекает информацию о сущностях, используя только контекст, является
слово2век. Входные данные для word2vec — это набор предложений, а выходные данные — вложение для каждого слова. Подобно тому, как текст описывает контекст каждого слова через окружающие его слова, графы описывают контекст каждого узла через соседние узлы.
В то время как в тексте слова появляются в линейном порядке, на графиках это не так. Между соседними узлами нет естественного порядка. Итак, мы не можем использовать word2vec… Или можем?
Мы можем применить преобразование графической структуры наших данных к линейной структуре, чтобы информация, закодированная в графической структуре, не была потеряна. При этом мы сможем использовать старый добрый word2vec.
Ключевым моментом является выполнение случайных блужданий по графу. Каждый обход начинается со случайного узла и выполняет серию шагов, где каждый шаг идет к случайному соседу. Каждое случайное блуждание формирует предложение, которое можно передать в word2vec. Этот алгоритм называется node2vec. Более подробная информация о процессе, о которой вы можете прочитать в оригинальная бумага.
Система рекомендации контента Taboola собирает множество данных, некоторые из которых могут быть представлены в графическом виде. Давайте рассмотрим один тип данных в качестве примера использования node2vec.
Taboola рекомендует статьи в виджете, отображаемом на веб-сайтах издателей:

В каждой статье есть именованные сущности — сущности, описанные заголовком. Например, пункт «самые милые собаки на планете» содержит сущности «собака» и «планета». Каждая именованная сущность может появляться во многих различных элементах.
Мы можем описать эту связь с помощью графа следующим образом: каждый узел будет именованным объектом, и между двумя узлами будет ребро, если два именованных объекта появятся в одном и том же элементе:
Теперь, когда мы можем описать наши данные графически, давайте запустим node2vec, чтобы посмотреть, какие идеи мы можем извлечь из данных. Вы можете найти рабочий код здесь.
Изучив встраивания узлов, мы можем использовать их в качестве функций для последующей задачи, например, прогнозирования CTR (Click Through Rate). Хотя это может принести пользу модели, будет трудно понять качества, полученные node2vec.
Другим вариантом было бы сгруппировать похожие вложения вместе, используя
К-означаети раскрасьте узлы в соответствии с их связанным кластером:

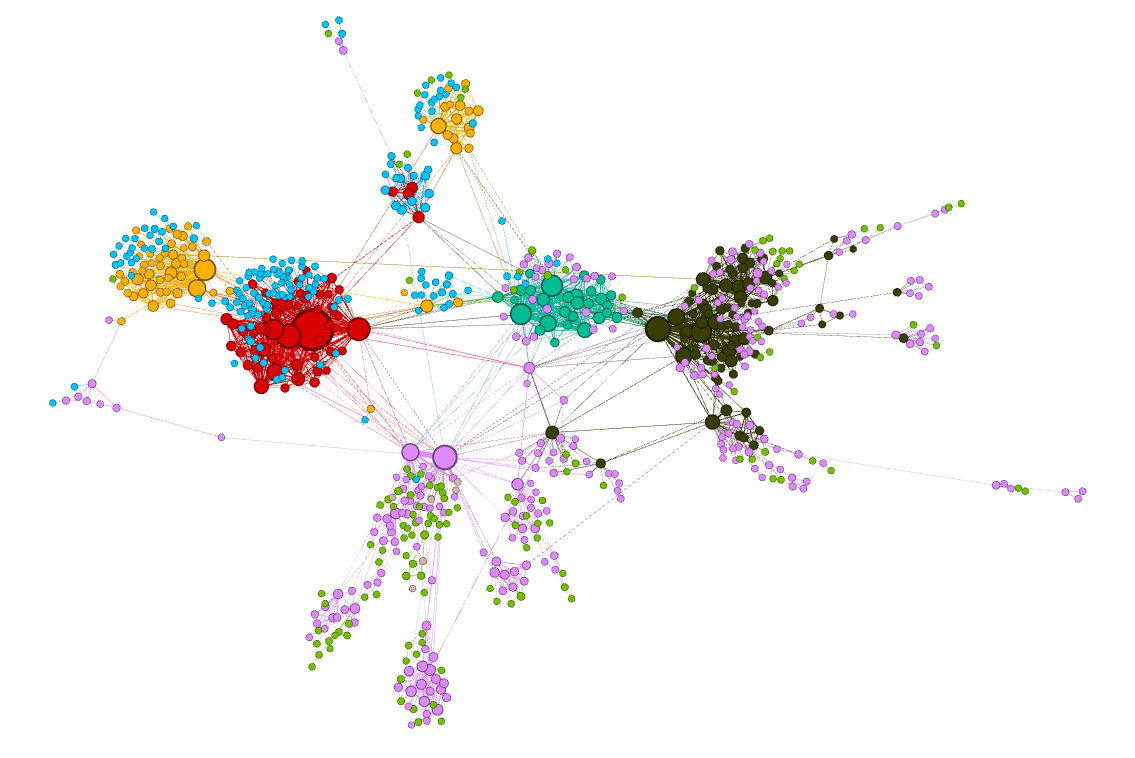
Прохладный! Кластеры, захваченные node2vec, кажутся однородными. Другими словами, узлы, которые находятся близко друг к другу в графе, также близки друг к другу в пространстве вложения. Возьмем, к примеру, оранжевый кластер — все его именованные сущности связаны с баскетболом.
Вы можете задаться вопросом, в чем преимущество использования node2vec по сравнению с классическими графическими алгоритмами, такими как алгоритмы обнаружения сообщества (например, Алгоритм Гирвана-Ньюмена). Захват сообщества, к которому принадлежит каждый узел, определенно может быть выполнен с использованием таких алгоритмов, в этом нет ничего плохого. Собственно, это и есть фиче-инжиниринг. И мы уже знаем, что DL может сэкономить вам время на тщательную ручную разработку таких функций. Так почему бы не воспользоваться этим преимуществом? Мы также должны помнить, что node2vec изучает многомерные вложения. Эти вложения намного богаче, чем просто принадлежность к сообществу.
Использование node2vec в этом случае может быть не первой идеей, которая приходит на ум. Можно было бы предложить просто использовать word2vec, где каждое предложение представляет собой последовательность именованных сущностей внутри одного элемента. В этом подходе мы не рассматриваем данные как имеющие графическую структуру. Итак, в чем разница между этим подходом — который является допустимым, и node2vec?
Если подумать, каждое предложение, которое мы генерируем в подходе word2vec, — это прогулка по графу, который мы определили ранее. node2vec также определяет блуждания по тому же графу. Так они одинаковые, да? Давайте посмотрим на кластеры, которые мы получаем с помощью подхода word2vec:
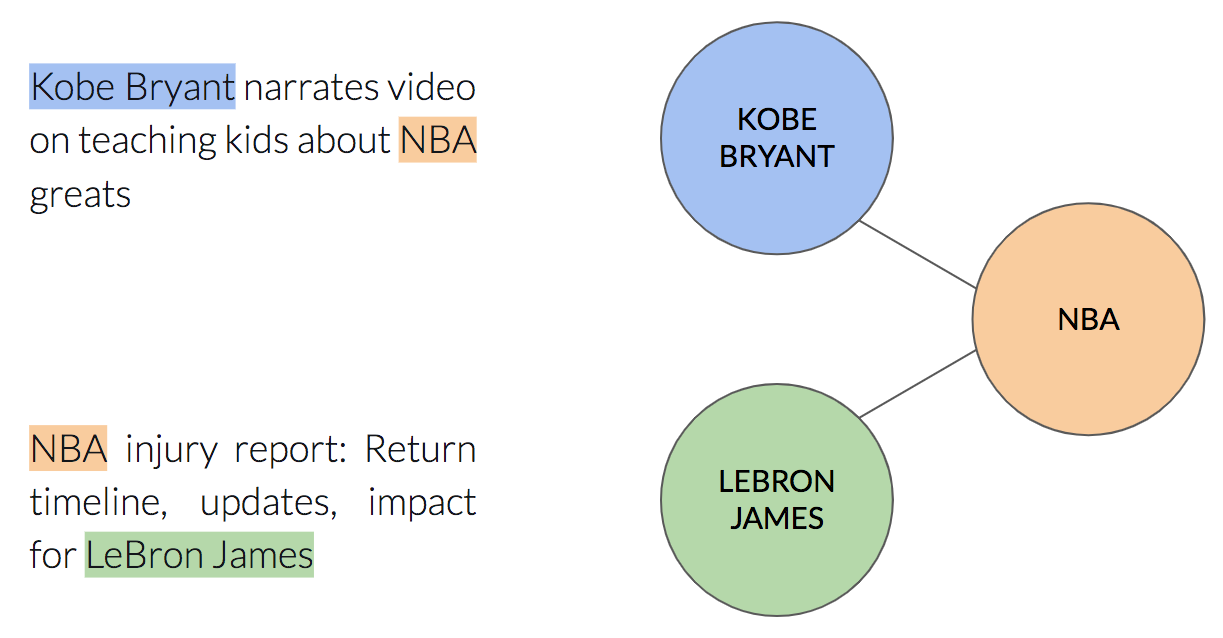
Теперь кластер «баскетбол» менее однороден — в нем есть и оранжевые, и синие узлы. Например, названная сущность «Баскетбол» была окрашена в оранжевый цвет, а баскетболисты «Леброн Джеймс» и «Коби Брайант» — в синий!

Но почему это произошло?
В этом подходе каждый проход в графе состоит только из именованных сущностей, которые появляются вместе в одном элементе. Это означает, что мы ограничены обходами, не превышающими расстояние 1 от начального узла. В node2vec у нас нет этого ограничения.
Поскольку в каждом подходе используются разные виды блужданий, изученные вложения собирают информацию разного типа.
Чтобы сделать это более конкретным, рассмотрим следующий пример: скажем, у нас есть два элемента — один с именованными объектами A, B, C, а другой с D, B, E. Эти элементы вызывают следующий граф:
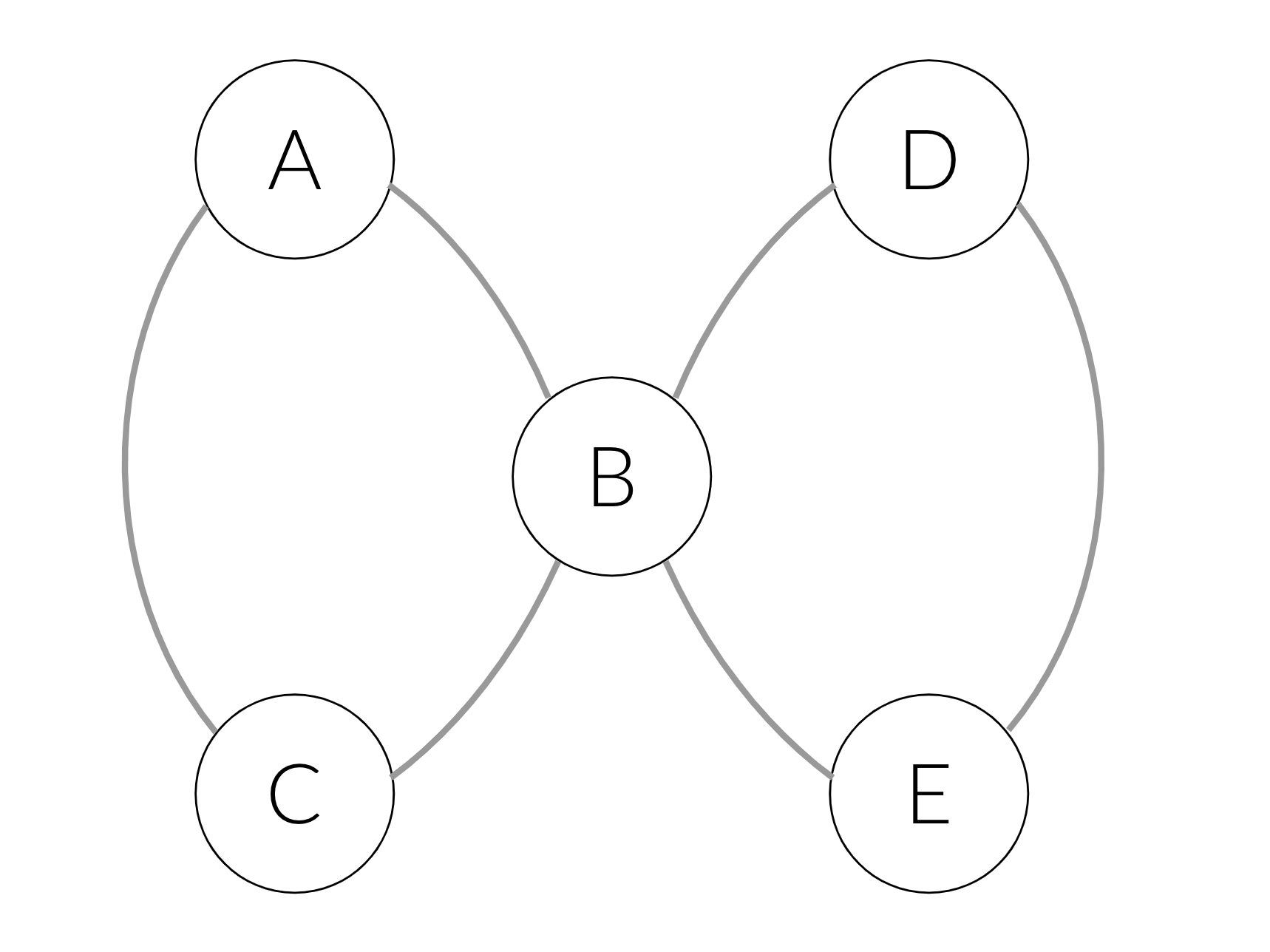
В простом подходе word2vec мы создадим следующие предложения: (A, B, C) и (D, B, E). В подходе node2vec мы также можем получить такие предложения, как (A, B, E). Если мы вытащим последний в процесс обучения, то узнаем, что E и C взаимозаменяемы: префикс (A, B) сможет предсказать и C, и E. Следовательно, C и E получат аналогичные вложения, и будут быть сгруппированы вместе.
Важно использовать правильную структуру данных для представления ваших данных. Каждая структура данных подразумевает свой алгоритм обучения или, другими словами, вводит разное индуктивное смещение.
Идентификация ваших данных имеет определенную структуру, поэтому вы можете использовать правильный инструмент для работы, что может быть непросто.
Поскольку так много наборов данных реального мира естественным образом представлены в виде графиков, мы считаем, что графовые нейронные сети должны быть в нашем наборе инструментов для специалистов по данным.
Первоначально опубликовано на
Engineering.taboola.com
мной и Зоар Комаровский.